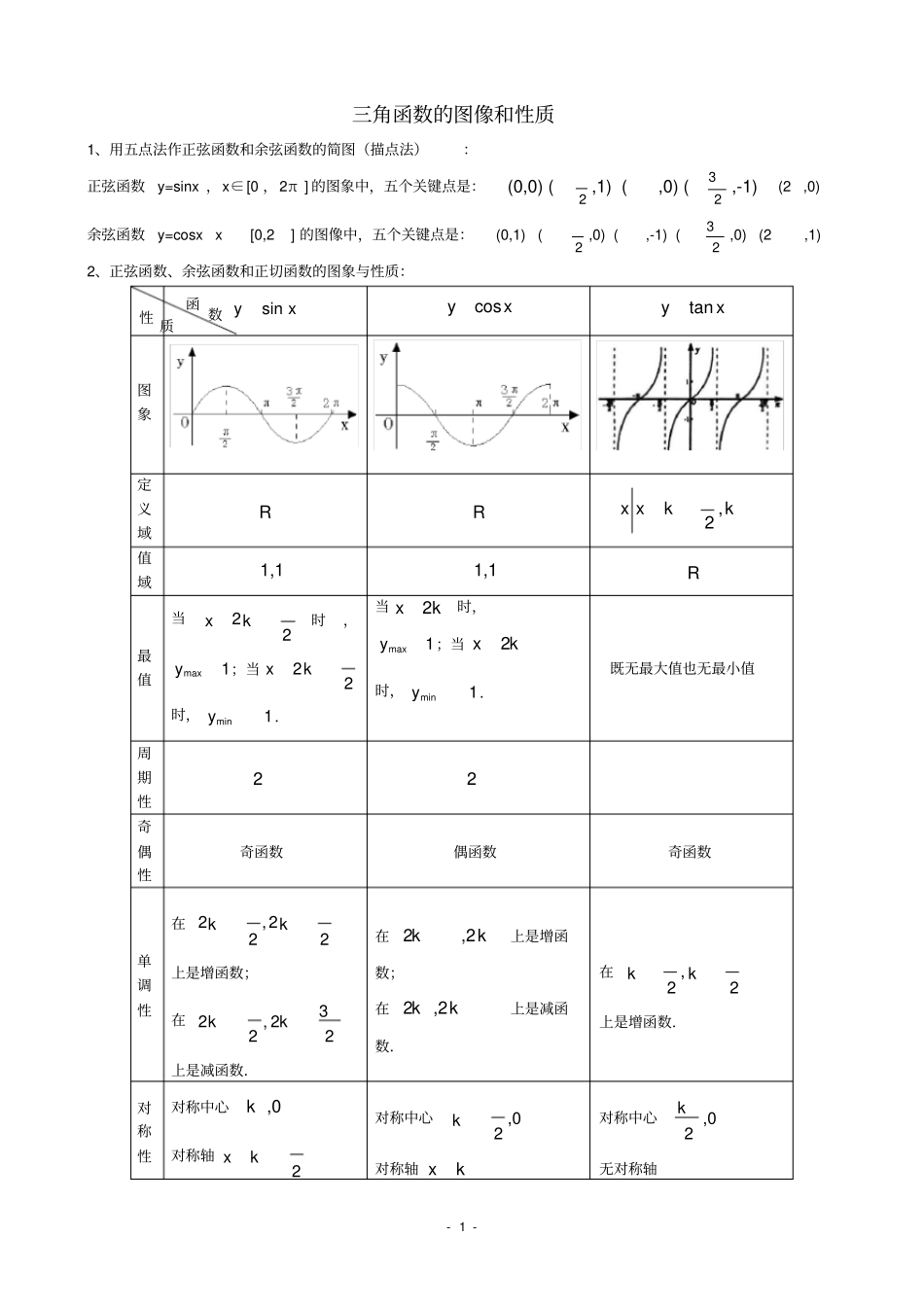
-1-三角函数的图像和性质1、用五点法作正弦函数和余弦函数的简图(描点法):正弦函数y=sinx,x∈[0,2π]的图象中,五个关键点是:(0,0)(2,1)(,0)(23,-1)(2,0)余弦函数y=cosxx[0,2]的图像中,五个关键点是:(0,1)(2,0)(,-1)(23,0)(2,1)2、正弦函数、余弦函数和正切函数的图象与性质:sinyxcosyxtanyx图象定义域RR,2xxkk值域1,11,1R最值当22xk时,max1y;当22xk时,min1y.当2xk时,max1y;当2xk时,min1y.既无最大值也无最小值周期性22奇偶性奇函数偶函数奇函数单调性在2,222kk上是增函数;在32,222kk上是减函数.在2,2kk上是增函数;在2,2kk上是减函数.在,22kk上是增函数.对称性对称中心,0k对称轴2xk对称中心,02k对称轴xk对称中心,02k无对称轴函数性质-2-例作下列函数的简图(1)y=|sinx|,x∈[0,2π],(2)y=-cosx,x∈[0,2π]例利用正弦函数和余弦函数的图象,求满足下列条件的x的集合:21sin)1(x21cos)2(x3、周期函数定义:对于函数()yfx,如果存在一个非零常数T,使得当x取定义域内的每一个值时,都有:()()fxTfx,那么函数()yfx就叫做周期函数,非零常数T叫做这个函数的周期。注意:周期T往往是多值的(如sinyx2,4,⋯,-2,-4,⋯都是周期)周期T中最小的正数叫做()yfx的最小正周期(有些周期函数没有最小正周期)sinyx,cosyx的最小正周期为2(一般称为周期)正弦函数、余弦函数:2T。正切函数:例求下列三角函数的周期:1y=sin(x+3)2y=cos2x3y=3sin(2x+5)4y=tan3x例求下列函数的定义域和值域:(1)2sinyx(2)3sinyx(3)lgcosyx-3-例5求函数sin(2)3yx的单调区间例不求值,比较大小(1)sin(-18)、sin(-10);(2)cos(-523)、cos(-417).解:(1) -2<-10<-18<2.(2)cos(-523)=cos523=cos53且函数y=sinx,x∈[-2,2]是增函数cos(-417)=cos417=cos4∴sin(-10)<sin(-18) 0<4<53<π即sin(-18)-sin(-10)>0且函数y=cosx,x∈[0,π]是减函数∴cos53<cos4即cos53-cos4<0∴cos(-523)-cos(-417)<04、函数sin0,0yx的图像:(1)函数sin0,0yx的有关概念:①振幅:;②周期:2;③频率:12f;④相位:x;⑤初相:.(2)振幅变换①y=Asinx,xR(A>0且A1)的图象可以看作把正数曲线上的所有点的纵坐标伸长(A>1)或缩短(0
0且ω1)的图象,可看作把正弦曲线上所有点的横坐标缩短(ω>1)或伸长(0<ω<1)到原来的1倍(纵坐标不变)②若ω<0则可用诱导公式将符号“提出”再作图ω决定了函数的周期,这一变换称为周期变换(4)相位变换-4-一般地,函数y=sin(x+),x∈R(其中≠0)的图象,可以看作把正弦曲线上所有点向左(当>0时)或向右(当<0时=平行移动||个单位长度而得到(用平移法注意讲清方向:“加左”“减右”)y=sin(x+)与y=sinx的图象只是在平面直角坐标系中的相对位置不一样,这一变换称为相位变换5、小结平移法过程(步骤)6、函数sinyx,当1xx时,取得最小值为miny;当2xx时,取得最大值为maxy,则maxmin12yy,maxmin12yy,21122xxxx.例如图e,是f(x)=Asin(ωx+φ),A>0,|φ|<2的一段图象,则f(x)的表达式为例如图b是函数y=Asin(ωx+φ)+2的图象的一部分,它的振幅、周期、初相各是()AA=3,T=34,φ=-6BA=1,T=34,φ=-43CA=1,T=32,φ=-43DA=1,T=34,φ=-6作y=sinx(长度为2的某闭区间)得y=sin(x+φ)得y=sinωx得y=sin(ωx+φ)得y=sin(ωx+φ)得y=Asin(ωx+φ)的图象,先在一沿x轴平移|φ|个单位横坐标伸长或缩短横坐标伸长或缩短沿x轴平移||个单位纵坐标伸长或缩短纵坐标伸长或缩短图e-5-例画出函数y=3sin(2x+3),x∈R的简图解:(五点法)由T=22,得T=π列表:x–6123127652x+302π232π3sin(2x+3)030–30例求函数33tanxy的定义域、值域,并指出它的周期性、奇偶性、单调性解:由233kx得1853kx,所求定义域为zkkxRxx,1853,|且值域为R,周期3T,是非奇非偶函数在区间zkkk1853,183上是增函数例已知函数y...