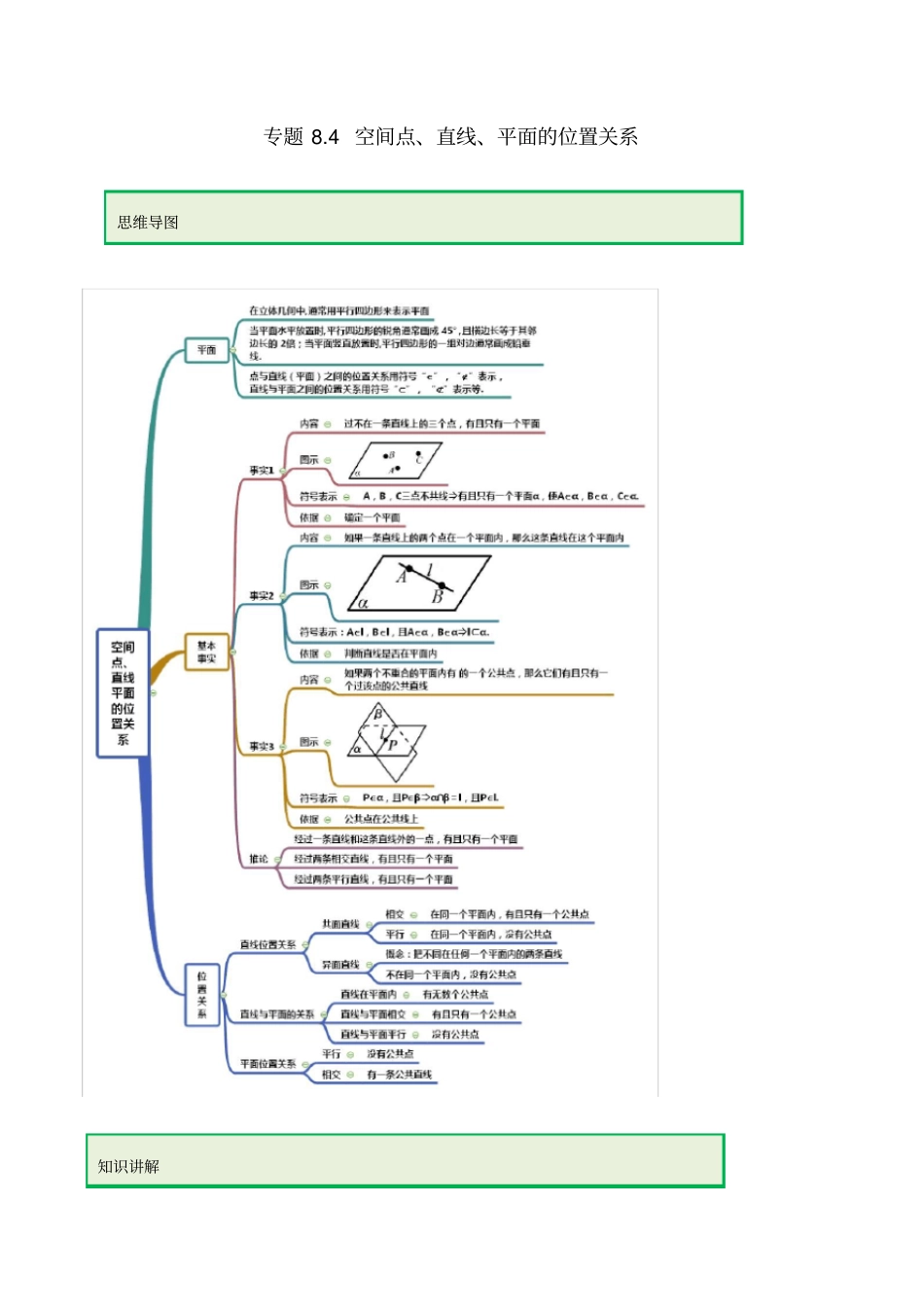
专题8.4空间点、直线、平面的位置关系知识讲解思维导图运用一基本事实辨析【例1】(1)(2019·安徽高二月考)下列说法错误的是()A.平面与平面相交,它们只有有限个公共点B.经过一条直线和这条直线外的一点,有且只有一个平面C.经过两条相交直线,有且只有一个平面D.如果两个平面有三个不共线的公共点,那么这两个平面重合(2)下列结论中不正确的是()A.若两个平面有一个公共点,则它们有无数个公共点B.若已知四个点不共面,则其中任意三点不共线C.若点A既在平面内,又在平面内,则与相交于b,且点A在b上D.任意两条直线不能确定一个平面【答案】(1)A(2)D【解析】A.平面与平面相交,它们只有有限个公共点平面与平面相交成一条直线,因此它们有无限个公共点.A错误.B.经过一条直线和这条直线外的一点,有且只有一个平面直线和直线外一点确定一个平面,B正确C.经过两条相交直线,有且只有一个平面两条相交直线确定一个平面,C正确D.如果两个平面有三个不共线的公共点,那么这两个平面重合不共线的三点确定一个平面,D正确故答案选A.(2)由平面基本性质可知,若两个不重合的平面有一个公共点,则两平面相交于过这一点的一条直线,有无数个公共点,因此选项A,C正确;当平面四个点中,有三点共线,由直线与直线外一点确定一个平面可得此四个点共面,故假设不成立,即其中任意三点不共线,因此选项B正确;若两条直线平行或相交,则可以确定一个平面,因此选项D错误.故选D.【举一反三】1.(2019·山西高二月考)下列命题中,真命题的个数为()①如果两个平面有三个不在一条直线上的公共点,那么这两个平面重合;②两条直线可以确定一个平面;③空间中,相交于同一点的三条直线在同一平面内;④若M∈α,M∈β,α∩β=l,则M∈l.A.1B.2C.3D.4【答案】B【解析】由公理二知命题①④正确;命题②两条直线异面时不成立,为假命题;命题③空间中,相交于同一点的三条直线可能确定三个平面,为假命题。故选B2.(2019·贵州省铜仁第一中学)在下列命题中,不是公理的是()A.过不在同一条直线上的三点,有且只有一个平面B.平行于同一个平面的两个平面相互平行C.如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在此平面内D.如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线【答案】B【解析】对于A,过不在同一条直线上的三点,有且只有一个平面,是公理2;对于B,平行于同一个平面的两个平面相互平行,不是公理;对于C,如果一条直线上的两点在一个平面内,那么这条直线在此平面内,是公理1;对于D,如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线,是公理3.故选:B.3.(2019·浙江高二期末)设P表示一个点,a,b表示两条直线,,表示两个平面,给出下列四个命题,其中正确的命题是()①,PaPa②,abPba③a∥b,,,aPbPb④,,bPaPPb.A.①②B.②③C.①④D.③④【答案】D【解析】当aP时,,PaP,但a∴①错;当a∩β=P时,②错;如图 a∥b,P∈b,∴Pa,∴由直线a与点P确定唯一平面α,又a∥b,由a与b确定唯一平面β,但β经过直线a与点P∴β与α重合,∴b?α,故③正确;两个平面的公共点必在其交线上,故④正确.故选:D.4.一条直线和这条直线之外不共线的三点所能确定的平面的个数是()A.1或3B.1或4C.3或4D.1、3或4【答案】D【解析】直线之外不共线的三点记为A,B,C.当直线在A,B,C所确定的平面内时,它们只能够只确定一个平面;当A,B,C三点中有两点与直线共面时,能确定平面有3个;当A,B,C三点中没有两点与直线共面时,这样可确定的平面最多就可以达到4个.故选:D.5.(2018·内蒙古集宁一中高一月考)空间四边形ABCD,E,F点分别是AB,BC的中点,G,H分别在CD和AD上,且满足2CGAHGDHD。(1)证明:E,F,G,H四点共面;(2)证明:EH,FG,BD三线共点.【答案】(1)见解析;(2)见解析.【解析】(1)由题意,,EF分别为,ABBC的中点,所以//EFAC,又由CGAHGDHD,根据平行线段成比例,可得//GHAC,所以//EFGH,所以四点,,,EFGH在同一平面内,即,,,EFGH四点共面。(2)由题意,,EF分别为,ABBC的...