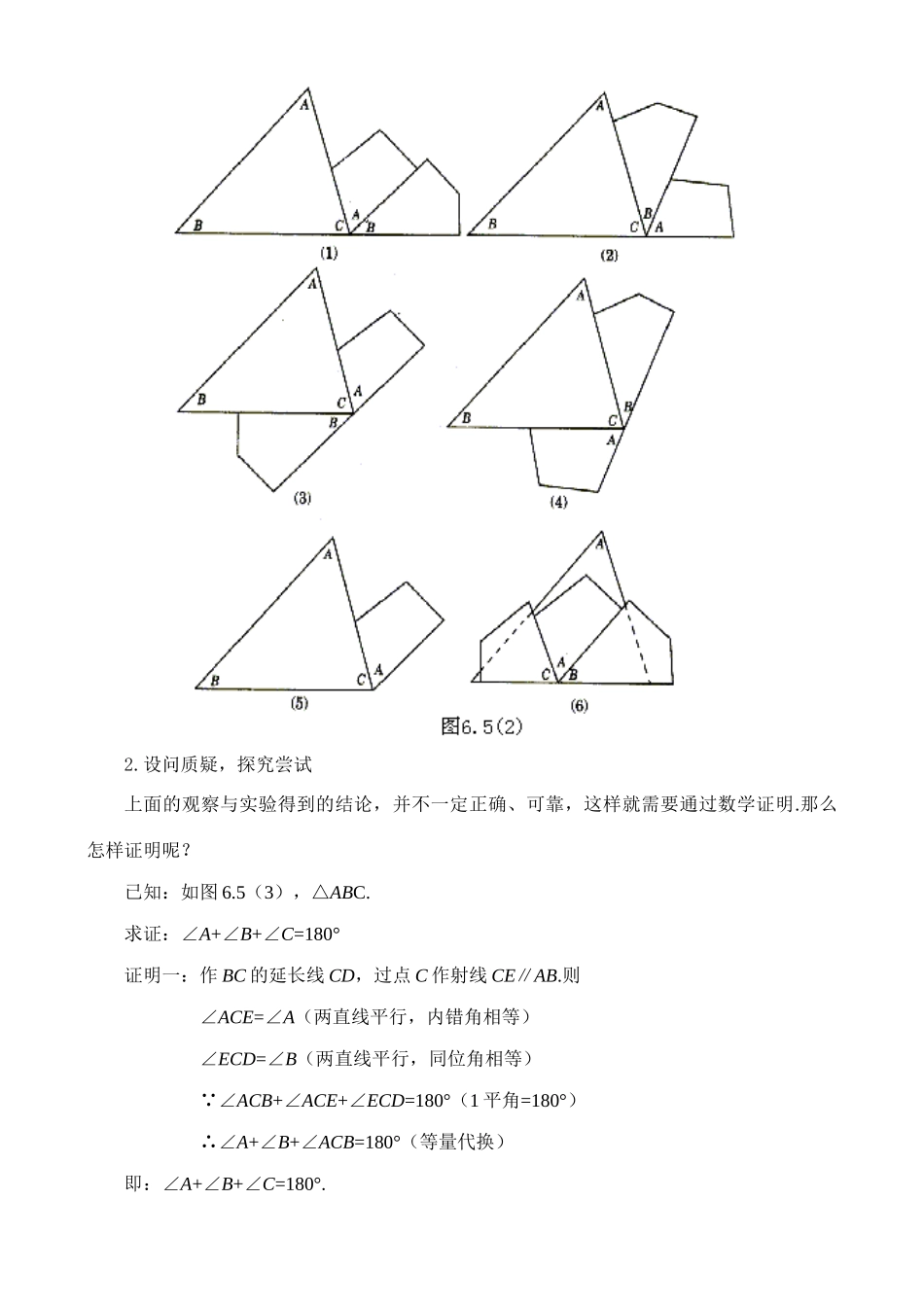
§6.5三角形内角和定理的证明教学目标1.知识目标:三角形的内角和定理的证明.2.能力目标:通过三角形内角和定理的证明,学会添加辅助线.3.情感目标:通过三角形内角和定理的证明,激发学生的数学兴趣.教学重点三角形内角和定理的证明.教学难点三角形内角和定理的证明方法.教学方法引导探索法教学过程1.创设情境,自然引入小学里,我们曾用量角器量出三角形三个内角的具体度数后计算它们的和;也曾用折叠一张三角形纸片,把三角形的三个内角拼在一起,如图6.5(1)将一张三角形纸片折叠拼合演示),得到“三角形三个内角的和等于180°”的结论其实,拼出∠A+∠B+∠C=180°的方法有多种多样,如图6.5(2)2.设问质疑,探究尝试上面的观察与实验得到的结论,并不一定正确、可靠,这样就需要通过数学证明.那么怎样证明呢?已知:如图6.5(3),△ABC.求证:∠A+∠B+∠C=180°证明一:作BC的延长线CD,过点C作射线CE∥AB.则∠ACE=∠A(两直线平行,内错角相等)∠ECD=∠B(两直线平行,同位角相等) ∠ACB+∠ACE+∠ECD=180°(1平角=180°)∴∠A+∠B+∠ACB=180°(等量代换)即:∠A+∠B+∠C=180°.证明二:作BC的延长线CD,作∠ECD=∠B.则:EC∥AB(同位角相等,两直线平行)∴∠A=∠ACE(两直线平行,内错角相等) ∠ACB+∠ACE+∠ECD=180°(1平角=180°)∴∠ACB+∠A+∠B=180°(等量代换)证明三:如图6.5(4) PQ∥BC(已作)∴∠PAB=∠B(两直线平行,内错角相等)∠QAC=∠C(两直线平行,内错角相等) ∠PAB+∠BAC+∠QAC=180°(1平角=180°)∴∠B+∠BAC+∠C=180°(等量代换)证明四:如图6.5(5)在BC上任取一点D,过点D分别作DE∥AB交AC于E,DF∥AC交AB于F.∴四边形AFDE是平行四边形(平行四边形的定义)∠BDF=∠C(两直线平行,同位角相等)∠EDC=∠B(两直线平行,同位角相等)∴∠EDF=∠A(平行四边形的对角相等) ∠BDF+∠EDF+∠EDC=180°(1平角=180°)∴∠A+∠B+∠C=180°(等量代换)证明五:如图6.5(6),作CA的延长线AD,过点A作∠DAE=∠C(过程略)证法六:如图6.5(7),过点A任作一条射线AD,再作BE∥AD,CF∥AD. BE∥AD∥CF∴∠1=∠3,∠2=∠4,∠EBC+∠BCF=180°∴∠BAC+∠ABC+∠ACB=∠EBC+∠BCF=180°.3.变式训练,巩固提高(1)已知:如图6.5(8),在△ABC中,DE∥BC,∠A=60°,∠C=70°,求证:∠ADE=50°(2)已知:如图6.5(9),在△ABC中,∠A=n°,∠ABC、∠ACB的平分线交于点O,求证:∠BOC=90°+n°4.总结串联,巩固提高(1)三角形内角和定理,提示了三角形三个内角之间的一个确定的数量关系,所以求解一个三角形的三个内角,只要再给出两个条件即可。(2)我们从多种拼图活动中找到了多种添画辅助线的方法,同时以三角形内角和定理的推证中,可以看出灵活、恰当的添画辅助线,有助于获得简捷、新颖、多样的解题途径。教学检测一.请你想一想1.在△ABC中:(l)已知∠A=80°,能否知∠B、∠C的度数?(2)已知∠A=80°,∠B=52°,则∠C=?(3)已知∠A=80°,∠B-∠C=40°,则∠C=?(4)已知∠A+∠B=100°,∠C=2∠A,能否求出∠A、∠B、∠C的度数。(5)已知∠A:∠B:∠C=1:3:5,能否求出∠A、∠B、∠C的度数?2.三角形三个内角可以都是锐角吗?都是直角吗?都是钝角吗?最多能有几个直角?最多能有几个钝角?二.请你来计算1.如图6.5(10),求∠A+∠B+∠C+∠D+∠E的度数。2.如图6.5(11),D是△ABC内任意一点,求证:∠ADB=∠1+∠2+∠C三.请你来证明1.已知:如图6.5(12),△ABC中,AD是高,E是AC边上一点,BE与AD交于点F,∠ABC=45°,∠BAC=75°,∠AFB=120°.求证:BE⊥AC.2.已知:如图6.5(13),△ABC中,∠B=∠ACB,CD是高,求证:∠BCD=∠A.参考答案一.请你想一想1.(1)不知道(2)∠C=48°(3)∠C=30°(4)∠A=40°,∠B=60°,∠C=80°(5)∠A=20°,∠B=60°,∠C=100°2.三角形三个内角可以都是锐角,不能都是直角,不能都是钝角,最多能有一个直角,最多能有一个钝角.二.请你来计算1.∠A+∠B+∠C+∠D+∠E=180°2.略三.请你来证明1.证明: AD是高(已知)∴∠A...