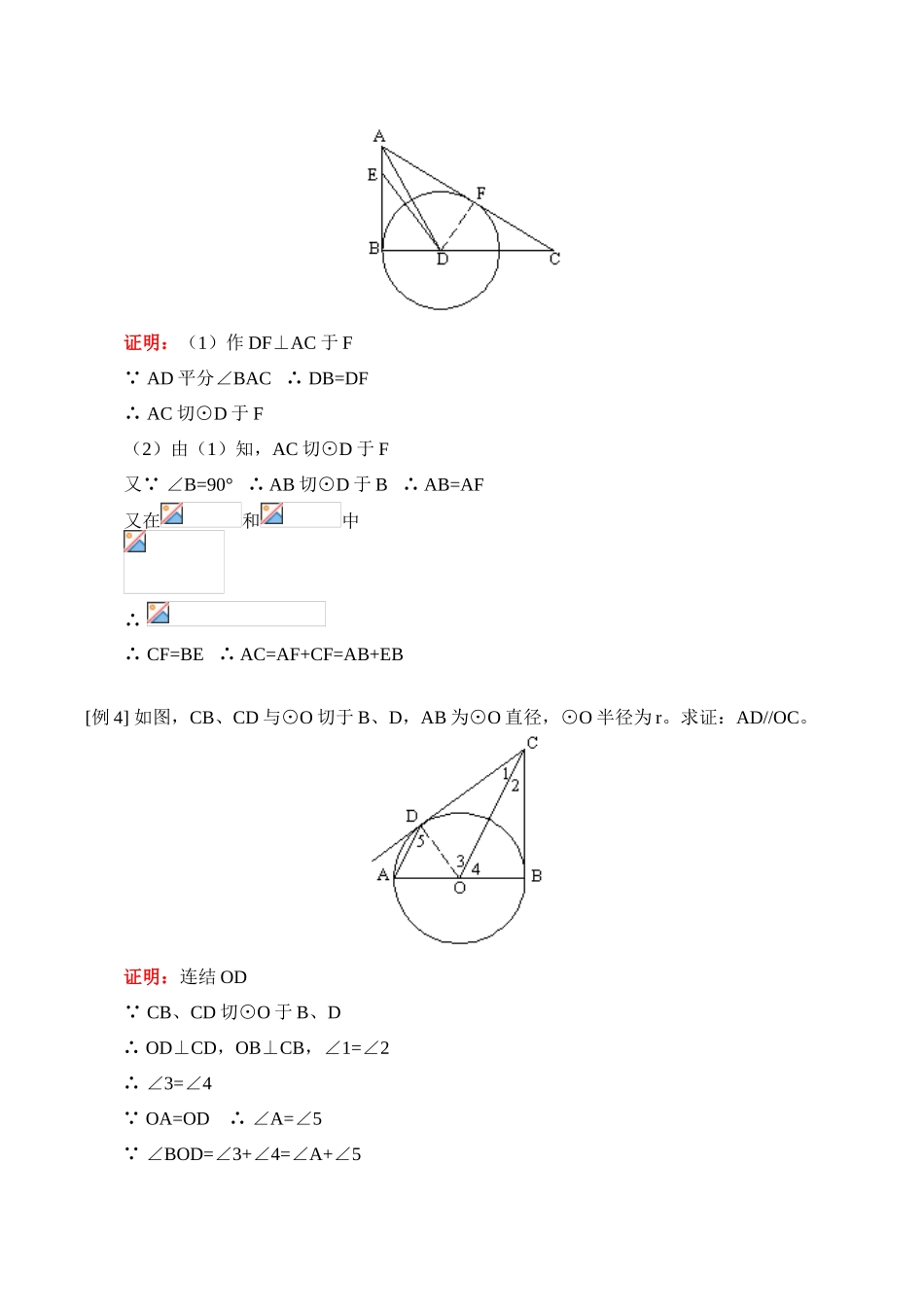
一.教学内容:切线长定理及其应用二.重点、难点:重点:切线长定理以及应用难点:切线长定理的题设、结论三.具体内容:1.切线长:经过圆外一点向圆引两条切线,在经过圆外一点的圆的切线上,这点和切点之间线段的长。2.切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这点的连线平分两切线的夹角。【典型例题】[例1]如图,⊙O分别切△ABC三边AB、BC、CA于点D、E、F,若BC=a,CA=b,AB=c,(1)求AD、BE、CF的长;(2)若∠C=90°,求△ABC内切圆半径r。解:(1)∵⊙O切△ABC三边AB、BC、CA于D、E、F∴AD=AF,BD=BE,CE=CF∴∵BC=a,CA=b,AB=c∴同理(2)连结OE、OF∵⊙O与AB、BC切于D、E∴OE⊥BC,OF⊥AC∵∠C=90°∴四边形OECF为矩形又∵OE=OF∴四边形OECF为正方形∴OE=OF=CE=CF由(1)知∴内切圆半径[例2]如图,⊙O切△ABC的边BC于D,切AB、AC延长线于E、F,△ABC的周长为18,求AE。解:由已知得CF=CD,BD=BE,AE=AF∴AB+AC+BC=AB+AC+CD+BD=AB+AC+CF+BE=AE+AF=2AE∵△ABC周长为18∴[例3]如图,在中,∠B=90°,∠A的平分线交BC于D,E为AB上一点,DE=DC,以D为圆心,DB为半径作⊙D,求证:(1)AC是⊙O切线;(2)AB+EB=AC。证明:(1)作DF⊥AC于F∵AD平分∠BAC∴DB=DF∴AC切⊙D于F(2)由(1)知,AC切⊙D于F又∵∠B=90°∴AB切⊙D于B∴AB=AF又在和中∴∴CF=BE∴AC=AF+CF=AB+EB[例4]如图,CB、CD与⊙O切于B、D,AB为⊙O直径,⊙O半径为r。求证:AD//OC。证明:连结OD∵CB、CD切⊙O于B、D∴OD⊥CD,OB⊥CB,∠1=∠2∴∠3=∠4∵OA=OD∴∠A=∠5∵∠BOD=∠3+∠4=∠A+∠5∴2∠3=2∠5∴∠3=∠5∴AD//OC[例5]如图,两同心圆O,PA、PB是大圆的两条切线,PC、PD是小圆的两条切线,A、B、C、D为切点,求证:AC=BD。证明:连结PO∵PA、PB为大圆切线∴PA=PB,∠APO=∠BPO又∵PC、PD为小圆切线∴PC=PD,∠CPO=∠DPO∴∠APC=∠APO-∠CPO=∠BPO-∠DPO=∠BPD∴在△PAC和△PBD中∴△PAC≌△PBD∴AC=BD[例6]如图,AB是⊙O直径,AD、BC、CD切⊙O于A、B、E,求证:OC⊥OD。证明:∵AD、BC、CD切⊙O于A、B、E∴DO平分∠ADE,CO平分∠BCE∴∠1=∠2=∠ADE,∠3=∠4=∠BCE∵AB是⊙O的直径,AD、BC切⊙O于A、B∴AB⊥AD,AB⊥BC∴AD//BC∴∠ADC+∠BCE=180°∴∠2+∠4=∠ADE+∠BCE=(∠ADE+∠BCE)=90°∴∠COD=90°∴OC⊥OD【模拟试题】1.如图,AB、AC是⊙O的切线,B、C为切点,D为上一点,且∠A=70°,则∠BDC=()A.250°B.120°C.125°D.115°2.如图,PQ、PR、AB是⊙O的切线,切点分别为Q、R、S,若∠APB=40°,则∠AOB=()A.50°B.60°C.70°D.80°3.如图,AB、AC分别切⊙O于B、C,AB=20,DE是⊙O的切线与AB、AC分别交于D、E两点,则△ADE的周长是()A.20B.40C.60D.804.PA、PB分别切⊙O于A、B,DE切⊙O于C,DE分别交线段PA、PB于D、E;若⊙O半径长为6cm,PO的长为10cm,则△PED的周长为。5.已知:⊙O的半径为4cm,PO=8cm,则过P点的⊙O的两条切线长为cm;这两条切线的夹角为。6.如图,PA、PB、DE分别与⊙O相切,若∠APB=68°,则∠DOE=,∠AOB=。试题答案1.C2.C3.B4.16cm5.;60°6.56°;112°