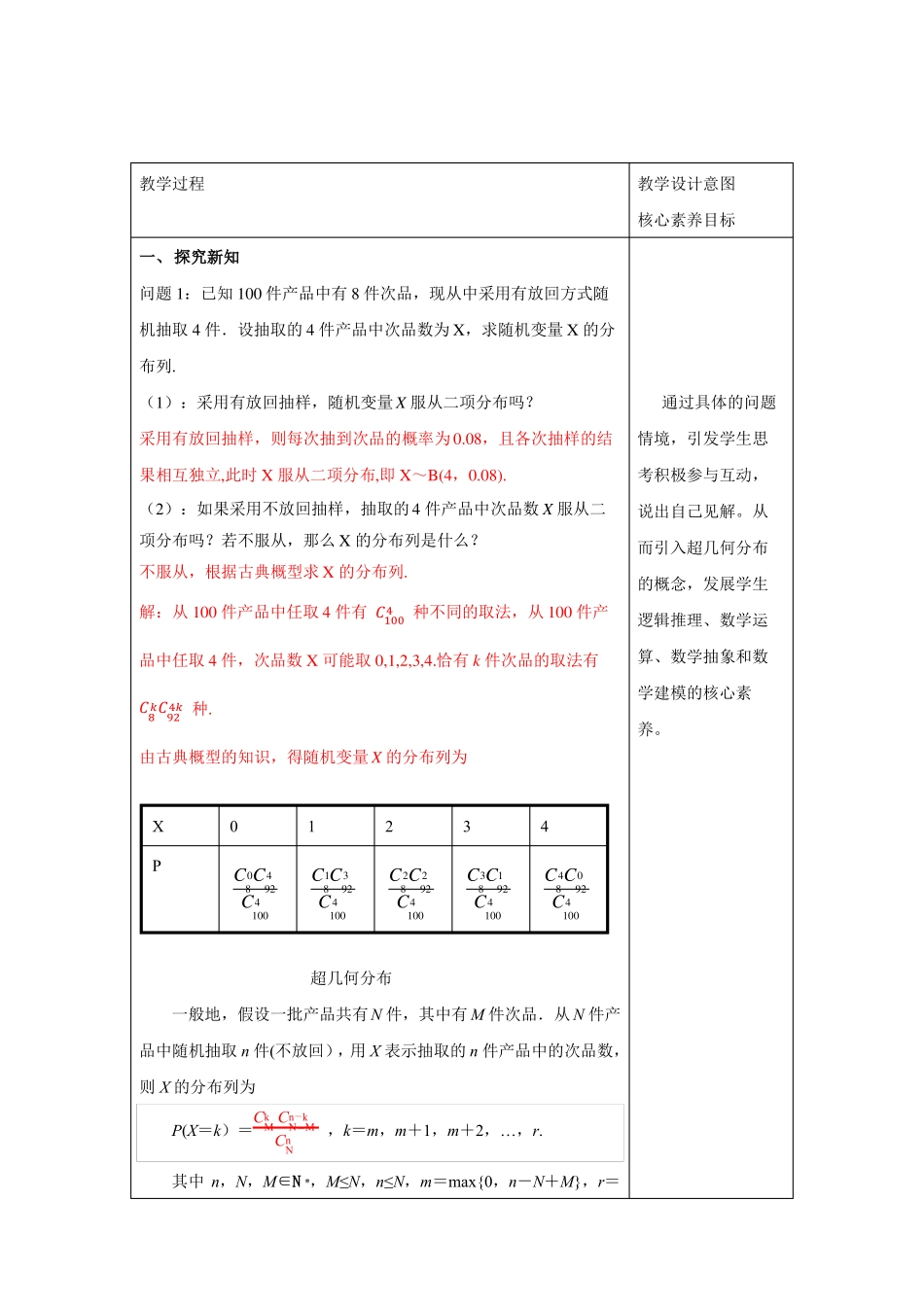
7.4.2超几何分布本节课选自《2019人教A版高中数学选择性必修第三册》,第七章《随机变量及其分布列》,本节课主本节课主要学习超几何分布超几何分布是一类应用广泛的概率模型,常常与二项分布问题综合运用,本节是学生已经学习了随机事件、等可能事件概率、互斥事件概率、条件概率和相互独立事件概率的求法、也学习了分布列的有关内容。它是对前面所学知识的综合应用。节课是从实际出发,通过抽象思维,建立数学模型,进而认知数学理论,应用于实际的过程。课程目标A.理解超几何分布,能够判定随机变量是否服从超几何分布;B.能够利用随机变量服从超几何分布的知识解决实际问题,会求服从超几何分布的随机变量的均值.重点:超几何分布的概念及应用难点:超几何分布与二项分布的区别与联系多媒体学科素养1.数学抽象:超几何分布的概念2.逻辑推理:超几何分布与二项分布的联系与区别3.数学运算:超几何分布的有关计算4.数学建模:模型化思想教学过程教学设计意图核心素养目标一、探究新知问题1:已知100件产品中有8件次品,现从中采用有放回方式随机抽取4件.设抽取的4件产品中次品数为X,求随机变量X的分布列.(1):采用有放回抽样,随机变量X服从二项分布吗?采用有放回抽样,则每次抽到次品的概率为0.08,且各次抽样的结果相互独立,此时X服从二项分布,即X~B(4,0.08).(2):如果采用不放回抽样,抽取的4件产品中次品数X服从二项分布吗?若不服从,那么X的分布列是什么?不服从,根据古典概型求X的分布列.4解:从100件产品中任取4件有𝐶100种不同的取法,从100件产通过具体的问题情境,引发学生思考积极参与互动,说出自己见解。从而引入超几何分布的概念,发展学生逻辑推理、数学运算、数学抽象和数学建模的核心素养。品中任取4件,次品数X可能取0,1,2,3,4.恰有k件次品的取法有𝑘4𝑘𝐶8𝐶92种.由古典概型的知识,得随机变量X的分布列为XP04C80C924C100113C8C924C10022C82C924C10031C83C924C10040C84C924C100超几何分布一般地,假设一批产品共有N件,其中有M件次品.从N件产品中随机抽取n件(不放回),用X表示抽取的n件产品中的次品数,则X的分布列为nkCkMCN-MP(X=k)=,k=m,m+1,m+2,…,r.CnN-其中n,N,M∈N*,M≤N,n≤N,m=max{0,n-N+M},r=min{n,M},则称随机变量X服从超几何分布.1.公式P(Xk)nkCkMCNM中个字母的含义nCNN—总体中的个体总数M—总体中的特殊个体总数(如次品总数)n—样本容量k—样本中的特殊个体数(如次品数)2.求分布列时可以直接利用组合数的意义列式计算,不必机械记忆这个概率分布列.3.“任取n件,恰有k件次品”是一次性抽取,用组合数列式.4.各对应的概率和必须为1.1.下列随机事件中的随机变量X服从超几何分布的是()A.将一枚硬币连抛3次,正面向上的次数XB.从7名男生与3名女生共10名学生干部中选出5名优秀学生干部,选出女生的人数XC.某射手射击的命中率为0.8,现对目标射击1次,记命中目标的次数为XD.盒中有4个白球和3个黑球,每次从中摸出1个球且不放回,X是首次摸出黑球时的总次数解析:由超几何分布的定义可知B正确.答案:B二、典例解析例1:从50名学生中随机选出5名学生代表,求甲被选中的概率.解:设X表示选出的5名学生中含甲的人数(只能取0或1),则X服从超几何分布,且N=50,M=1,n=5.因此,甲被选中的概率为14C1C1P(X1)549C5010例2.一批零件共有30个,其中有3个不合格,随机抽取10个零件进行检测,求至少有1件不合格的概率.解:设抽取的10个零件中不合格品数为𝑋,则𝑋服从超几何分布,且𝑁=30,𝑀=3,𝑛=10,𝑋的分布列为𝑃(𝑋=𝑘)=𝑘𝐶10𝑘𝐶32710𝐶30,𝑘=0,1,2,3通过问题分析,让学生掌握超几何分布的概念及其特点。发展学生逻辑推理,直观想象、数学抽象和数学运算的核心素养。至少有1件不合格的概率为𝑃(𝑋≥1)=𝑃(𝑋=1)+𝑃(𝑋=2)+𝑃(𝑋=3)371928𝐶3𝐶27𝐶3𝐶27𝐶3𝐶2795456146=10+10+10=++=≈0.7192203203203203𝐶30𝐶30𝐶30另解:(𝑋≥1)=1−𝑃(𝑋=0)=10𝐶10𝐶32710𝐶30=1203≈0.719257(1)当研究的事物涉及二维离散型随机变量(如:次品、两类颜色等问题)时的概率分布可视为一个超几何分布;(2)在超几何分布中,只要知道...