2431锐角三角函数VIP免费

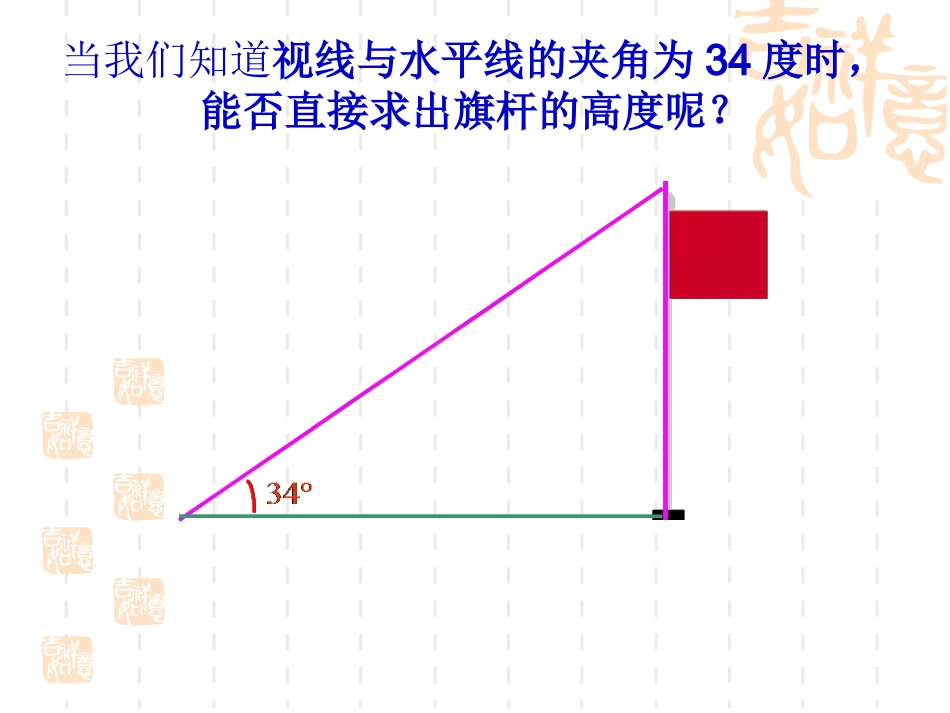
24.3锐角三角函数双桥中心学校尧义平BACA1B1C1△ABCA∽△1B1C11111CAACCBBC当我们知道视线与水平线的夹角为34度时，能否直接求出旗杆的高度呢？溫故知新:直角三角形ABC可以简记为RtABC△，你能说出各条边的名称吗？ab那么，RtABC△有哪些性质？c90BA角的性质：222cba边的性质：除了这些性质之外，那么边和角之间有没有联系呢？图19.3.1当∠A的大小确定以后，不管直角三角形大小如何变化，是否是一个固定的值的邻边的对边AAbaACBCP106B1C1RtABCRtAB△∽△1C1111ACACCBBC111ACCBACBC222ACACCBBC222ACCBACBCC2B2RtABCRtAB△∽△2C2所以＝________=________=111ACCB可见，在RtABC△中，对于锐角A的每一个确定的值，其对边与邻边的比值是惟一确定的.B2C2AC2tanA=的邻边的对边AAbaACBCtanA叫做∠A的正切函数想一想想一想对于锐角A的每一个确定的值，其对边与斜边、邻边与斜边、邻边与对边的比值也是惟一确定的吗？sinA=斜边的对边A222111ABCBABCBABBCcacbABACcosA=斜边的邻边AsinA叫做∠A的正弦函数cosA叫做∠A的余弦函数tanA叫做∠A的余切函数BCaACbtanA=AA的对边的邻边ACbBCacotA=AA的邻边的对边cotA叫做∠A的余切函数P106结论温馨提示：1、sinA不是一个角2、sinA不是sin与A的乘积3、sinA是一个比值4、sinA没有单位P107我们把sinA（正弦）cosA（余弦）tanA（正切）cotA（余切）统称为锐角∠A的三角函数例1、求出如图所示的RtABC△中∠A的四个三角函数值.1728922ACBCAB解：8178sinABBCA1715cosABACA158tanACBCA815cotBCACA思考：P1071、sinA和cosA的取值范围；2、sin2A+cos2A=?tanA.cotA=?下面让我们来掌握特殊角（30°45°60°）的三角函数值特殊角的三角函数值30°45°60°sinAcosAtanA1123233223222123P108P109例题2随堂练习1.12sin604cos303tan4523cos45tan302cot60.不用计算器，你能求出下列几个小题吗？；22.,23tan,,3?(,,?)B在△ABC中,A和B都是锐角,且sinA=那么这个三角形的形状是什么样的啊锐角三角形还是直角三角形或是钝角三角形啊5.:sin1AA拔高题已知一个三角形的三边长正好为、、cosA，且为锐角。现在，我想问的是这个三角形的形状是什么啊？根据这些条件你能判断出来吗？仔细考虑一下吧，看看能不能自己做出来？3.,90,3RtCABC在△ABC中斜边是直角边A的倍,则cosB为多少啊?3,53?tan,5?AAA4.你能根据sinA=求出锐角的其余的三个三角函数值吗若是知道你能求出这个时候锐角的其余的三个三角函数值吗我来试一试：1、如图1，在Rt△MNP中，∠N＝90゜.∠P的对边是_________,∠P的邻边是___________;∠M的对边是________,∠M的邻边是___________;2、求出如图2所示的Rt△DEC(∠E＝90゜)中∠D的四个三角函数值(用字母表示).3、设Rt△ABC，∠C＝90゜∠A、∠B、∠C的对边分别为a、b、c，根据下列所给条件∠B的四个三角函数值：（1）a=3，b=4；（2）a=5，c=13.MNPNPNMN4、如图，在RtABC△中，∠C＝90゜，sinA=,AB=15，求△ABC的周长和tanA的值.435、RtABC△中，如果各边都扩大到原来的两倍，则锐角A的正切值（）A、扩大到2倍B、缩小到2倍C、扩大到4倍D、没有变化ADBC图21312.B135.A6、如图2，ADCD,AB=13⊥，BC=12,CD=3,AD=4,则sinB=()53.C54.D7、已知：如图，△ABC中，∠ACB=90°，CD是高，AC=CD=，求∠BCD的四个三角函数值.62D知识回顾：本节课我学会了：1、2、……祝你进步……