正多边形和圆（第一课时）VIP免费

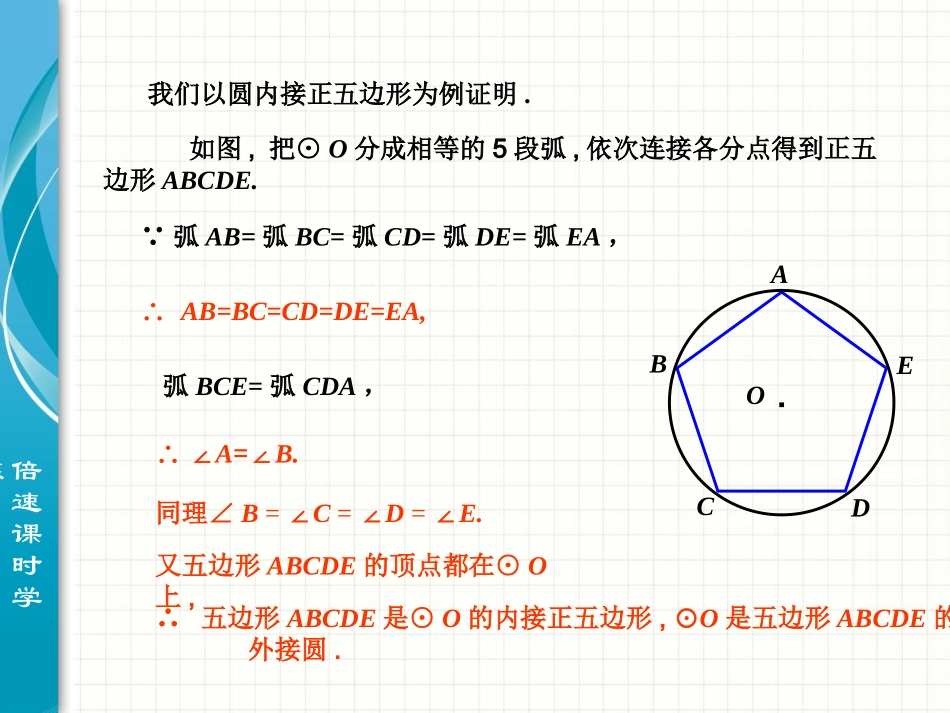
倍速课时学练如图,把⊙O分成相等的5段弧,依次连接各分点得到正五边形ABCDE.∴AB=BC=CD=DE=EA,∴∠A=∠B.·ABCDEO同理∠B=∠C=∠D=∠E.又五边形ABCDE的顶点都在⊙O上,∴五边形ABCDE是⊙O的内接正五边形,⊙O是五边形ABCDE的外接圆.我们以圆内接正五边形为例证明.∵弧AB=弧BC=弧CD=弧DE=弧EA，弧BCE=弧CDA，倍速课时学练正多边形每一边所对的圆心角叫做正多边形的中心角.O·中心角半径R边心距r我们把一个正多边形的外接圆的圆心叫做这个正多边形的中心.外接圆的半径叫做正多边形的半径.中心到正多边形的距离叫做正多边形的边心距.倍速课时学练例有一个亭子,它的地基是半径为4m的正六边形,求地基的周长和面积(精确到0.1m2).解:如图，由于ABCDEF是正六边形,所以它的中心角等于，△OBC是等边三角形，从而正六边形的边长等于它的半径.360606因此,亭子地基的周长l=4×6=24(m).在Rt△OPC中,OC=4,PC=4222BC，利用勾股定理,可得边心距224223.r亭子地基的面积211242341.6(m).22SlrOABCDEFRPr倍速课时学练归纳小结：正多边形的性质：（1）正多边形的一个内角等于（2）中心角：（3）正多边形的中心角等于外角的度数nno1802no360倍速课时学练练习1.矩形是正多边形吗?菱形呢?正方形呢?为什么?矩形不一定是正多边形.因为四条边不一定都相等;菱形不一定是正多边形.因为四个角不一定都相等;正方形是正多边形．因为四条边都相等，四个角都相等.倍速课时学练（1）正n边形的一个外角为30°，则它的边数为____，它的内角和为______；（2）如果一个正多边形的一个外角等于一个内角的三分之二，则这个正多边形的边数n=____；4．强化练习（3）正六边形的边长为1，则它的半径为_____，面积为________；（4）边长为1的正六边形的内切圆的面积是____．倍速课时学练2.各边相等的圆内接多边形是正多边形吗?各角都相等的圆内接多边形呢?如果是,说明为什么;如果不是,举出反例.各边相等的圆内接多边形是正多边形.多边形A1A2A3A4…An是⊙O的内接多边形,且A1A2=A2A3=A3A4=…=An－1An,123.nAAAA∴多边形A1A2A3A4…An是正多边形.A２A７An·A1A３A４A５A６O∴弧A1A2=弧A2A3=弧A3A4=…=弧An－1An=弧AnA1,∴弧A2A3An=弧A3A4A1=弧A4A5A2=…=弧A1A2An-1，倍速课时学练3.分别求出半径为R的圆内接正三角形，正方形的边长，边心距和面积.解：作等边△ABC的边BC上的高AD,垂足为D.连接OB，则OB=R.在Rt△OBD中，∠OBD=30°,边心距＝OD=1.2R在Rt△ABD中，∠BAD=30°,1322ADOAODRRR，2113333.2224ABCSBCADRRR·ABCDO由勾股定理，求得AB=R3倍速课时学练解：连接OB，OC，过点O作OE⊥BC垂足为E.则∠OEB=90°，∠OBE=∠BOE=45°.Rt△OBE为等腰直角三角形.则有222BEOEOB222OEOB222OBOE2222OEOBR边心距22222BCBERR边长2222ABCDSABBCRR正方形·ABCDOE