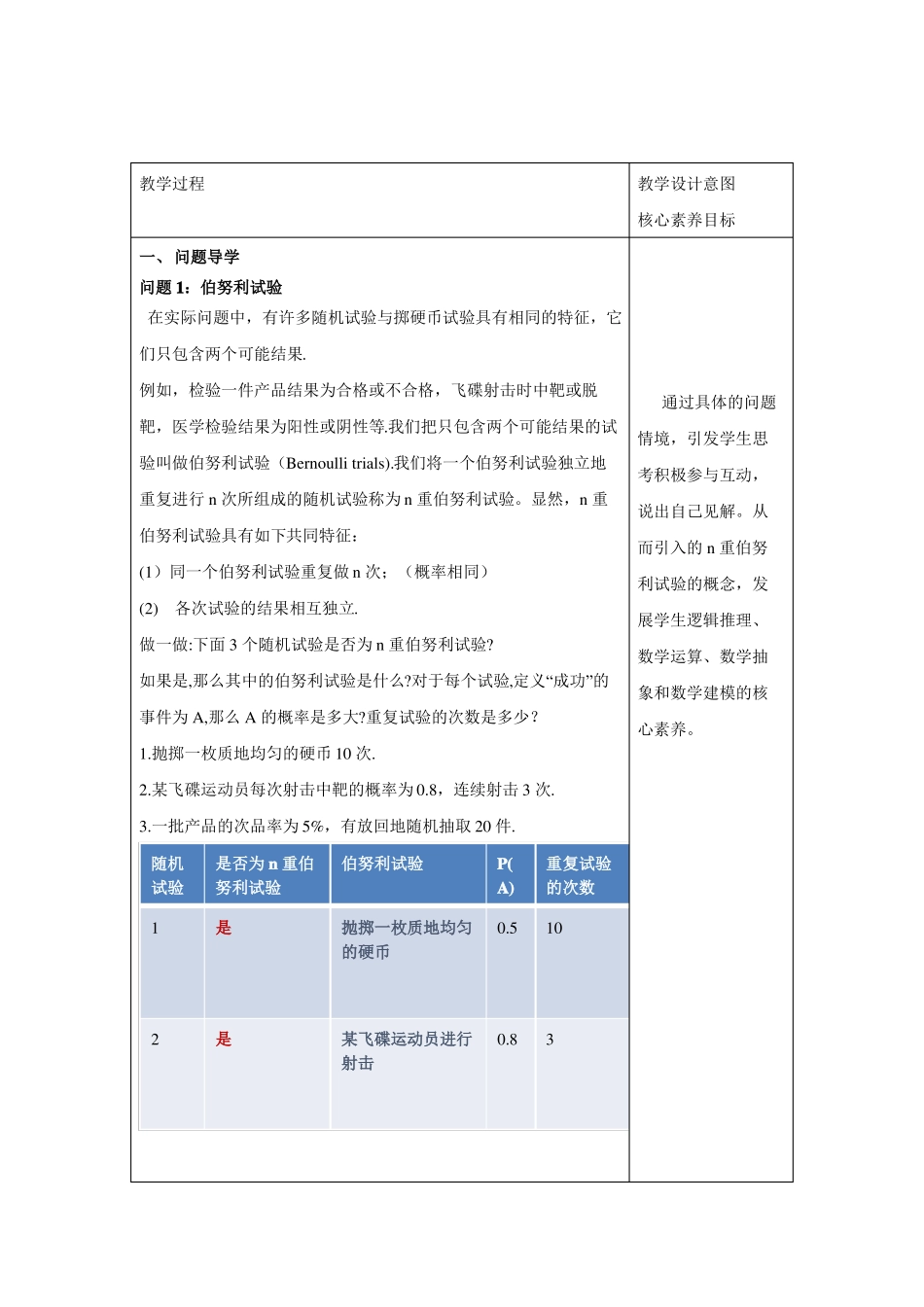
7.4.1二项分布本节课选自《2019人教A版高中数学选择性必修第三册》,第七章《随机变量及其分布列》,本节课主本节课主要学习二项分布前面学生已经掌握了有关概率的基础知识等可能事件概率、互斥事件概率、条件概率和相互独立事件概率的求法、也学习了分布列的有关内容。二项分布是一种应用广泛的概率模型,是对前面所学知识的综合应用。节课是从实际出发,通过抽象思维,建立数学模型,进而认知数学理论,应用于实际的过程。课程目标A.理解伯努利试验以及n重伯努利试验的概念,掌握随机变量服从二项分布的有关计算;B.能够解决随机变量服从二项分布的实际应用问题,会求服从二项分布的随机变量的均值和方差.重点:n重伯努利实验,二项分布及其数字特征;难点:在实际问题中抽象出模型的特征,识别二项分布.多媒体学科素养1.数学抽象:n重伯努利试验的概念2.逻辑推理:二项分布的随机变量的均值和方差3.数学运算:二项分布的有关计算4.数学建模:模型化思想教学过程教学设计意图核心素养目标一、问题导学问题1:伯努利试验在实际问题中,有许多随机试验与掷硬币试验具有相同的特征,它们只包含两个可能结果.例如,检验一件产品结果为合格或不合格,飞碟射击时中靶或脱靶,医学检验结果为阳性或阴性等.我们把只包含两个可能结果的试验叫做伯努利试验(Bernoullitrials).我们将一个伯努利试验独立地重复进行n次所组成的随机试验称为n重伯努利试验。显然,n重伯努利试验具有如下共同特征:(1)同一个伯努利试验重复做n次;(概率相同)(2)各次试验的结果相互独立.做一做:下面3个随机试验是否为n重伯努利试验?如果是,那么其中的伯努利试验是什么?对于每个试验,定义“成功”的事件为A,那么A的概率是多大?重复试验的次数是多少?1.抛掷一枚质地均匀的硬币10次.2.某飞碟运动员每次射击中靶的概率为0.8,连续射击3次.3.一批产品的次品率为5%,有放回地随机抽取20件.随机试验1是否为n重伯努利试验是伯努利试验P(A)0.5重复试验的次数10通过具体的问题情境,引发学生思考积极参与互动,说出自己见解。从而引入的n重伯努利试验的概念,发展学生逻辑推理、数学运算、数学抽象和数学建模的核心素养。抛掷一枚质地均匀的硬币2是某飞碟运动员进行射击0.833是从一批产品中随机抽取一件0.9520二、探究新知探究1:伯努利试验和n重伯努利试验有什么不同?伯努利试验是一个“有两个结果的试验”,只能关注某个事件发生或不发生;n重伯努利试验是对一个“有两个结果的试验”重复进行了n次,所以关注点是这n次重复试验中“发生”的次数X.进一步地,因为X是一个离散型随机变量,所以我们实际关心的是它的概率分布列.问题2:某飞碟运动员每次射击中靶的概率为0.8.连续3次射击,中靶次数X的概率分布列是怎样的?用A表示“第i次射击中靶”(i=1,2,3),用如下图的树状图表示试i验的可能结果:问题由分步乘法计数原理,3次独立重复试验共有2=8种可能结果,它们两两互斥,每个结果都是3个相互独立事件的积,由概率的加法公式和乘法公式得𝐴2𝐴3)=0.23,𝑃(𝑋=0)=𝑃(𝐴13𝐴2𝐴3)+𝑃(𝐴1𝐴2𝐴3)=3×0.8×0.22,𝑃(𝑋=1)=𝑃(𝐴1𝐴2𝐴3)+𝑃(𝐴1𝐴2𝐴3)=3×0.82×0.2,𝑃(𝑋=2)=𝑃(𝐴1𝐴2𝐴3)+𝑃(𝐴1𝐴2𝐴3)+𝑃(𝐴1P(X=3)=P(𝐴1𝐴2𝐴3)=0.83.为了简化表示,每次射击用1表示中靶,用0表示脱靶,那么3次射击恰好2次中靶的所有可能结果可表示为011,110,101,这三个结果发生的概率都相等,均为0.8×0.2,并且与哪两次中靶无关.2因此,3次射击恰好2次中靶的概率为𝐶3×0.82×0.2.同理可求中靶02次,1次,3次的概率.于是,中靶次数X的分布列为:𝑘𝑃(𝑋=𝑘)=𝐶3×0.8𝑘×0.23𝑘,𝑘=0,1,2,3探究2:如果连续射击4次,类比上面的分析,表示中靶次数X等于2的结果有哪些?写出中靶次数X的分布列.(1)表示中靶次数X等于2的结果有:𝐴1𝐴2𝐴3𝐴4,𝐴1𝐴2𝐴3𝐴4,,𝐴1𝐴2𝐴3𝐴4,𝐴1𝐴2𝐴3𝐴4,𝐴1𝐴2𝐴3𝐴4,𝐴1𝐴2𝐴3𝐴4,共6个。(2)中靶次数X的分布列为:𝑃(𝑋=𝑘)=0,1,2,3,4二项分布一般地,在n重伯努利试验中,设每次试验中事件A发生的概率为p(0