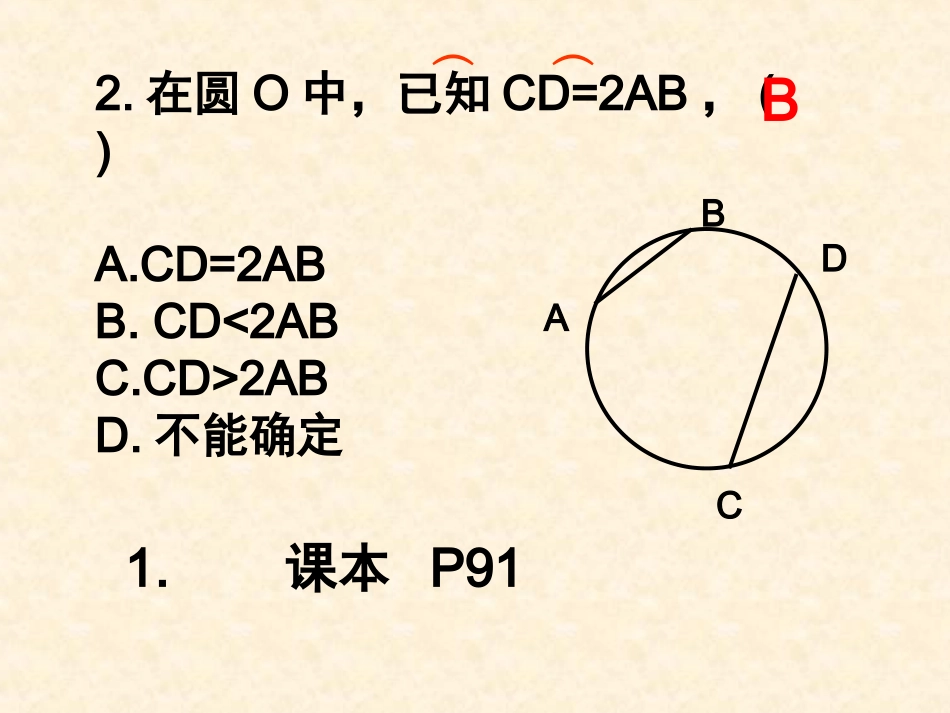
24.1.4圆周角(一)1、复习提问:(2)圆心角,弧,弦,弦心距关系定理是什么?(1)什么是圆心角?2.在圆O中,已知CD=2AB,()A.CD=2ABB.CD<2ABC.CD>2ABD.不能确定︵︵ABCDB1.课本P91∠ACB与∠AOB有何异同点?你知道∠ACB这一类的角名字吗?顶点在圆上,两边与圆相交的角,叫圆周角。圆周角的概念:BACO判断下列各图形中的是不是圆周角,并说明理由.归纳:一个角是圆周角的条件:①顶点在圆上;②两边都和圆相交.ABCO有没有圆周角?有没有圆心角?它们有什么共同的特点?它们都对着同一条弧⌒⌒⌒⌒探索研究:如果圆周角和圆心角对着同一条弧,那么这两个角存在怎样的关系?探究一:探究一:ABCO画一个圆,再任意画一个圆周角,看一下圆心在什么位置?圆心在一边上圆心在角内圆心在角外问题:圆周角的度数与相应的圆心角度数有什么关系?(1)当圆心在圆周角的一边上时,探探究究一:一:证明:(圆心在圆周角边上)结论:一条弧所对的圆周角等于它所对圆心角的一半.COBABACCOCOABOCBAC21CBACBOCABCOD提示:作射线AO交⊙O于D。转化为第1种情况证明:由第1种情况得∠即BAC=BOC∠21∠BAD=∠BOD21∠CAD=∠COD21∠BAD+∠CAD=∠BOD+∠COD21212.当圆心在圆周角内部时提示:能否转化为1的情况?证明:作射线AO交⊙O于D。由第1种情况得∠即BAC=BOC∠21∠BAD=∠BOD21∠CAD=∠COD21∠CAD-∠BAD=∠COD-∠BOD2121ABCOD3.当圆心在圆周角外部时圆周角定理推论1:同弧所对的圆周角相等OECDBA注意:圆周角与圆心角所对的弧必须是同弧或等弧ABCO一条弧所对的圆周角等于它所对的圆心角的一半。ABCO练习1:如图,已知在⊙O中,∠BOC=150°,求∠A练习2:已知:∠AOB=100°,求∠ACB的度数OCBA如果∠A=44°,则∠BOC=____.如果∠BOC=44°,则∠A=____.如果∠A=35°,则∠BDC=____.OABCD88°22°35°练习3练习4:如图,点A、B、C、D在同一个圆上,四边形ABCD的对角线把4个内角分成8个角,这些角中哪些是相等的角?D12345678ABC∠1=∠4∠2=∠7∠3=∠6∠5=∠8解:1.1.半圆或直径所对的圆周角等于多少度?推论推论22::半圆或直径所对的圆周角是半圆或直径所对的圆周角是90°(90°(直角直角).).90°90°的圆周角所对的弦是圆的直径的圆周角所对的弦是圆的直径探究二:探究二:OABC2.90°的圆周角所对的弦是否是直径?画板3练习1.如图AB是⊙O的直径,C,D是圆上的两点,若∠ABD=40°,则∠BCD=_____.ABOCD40°500练习2、如图,△ABC的顶点A、B、C都在⊙O上,∠C=30°,AB=2,则⊙O的半径是。CABO2例.如图⊙o的直径AB为10cm,弦AC为6cm,∠ACB的平分线交⊙o与D,求BC,AD,BD的长.ACBDO(2)在⊙o中,圆心角∠AOB=56°,则弦AB所对的圆周角等于多少?结论:一条弦所对的圆周角有两种,关系是相等或互补。一条弦所对的圆心角只有一个。练习.(1)在⊙o中,圆心角∠AOB=56°,则弧AB所对的圆周角等于多少?在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.顶点在圆上,两边与圆相交的角,叫圆周角.圆周角的概念:圆周角定理:推论:推论:((11)同弧或等弧所对圆周角都相等。)同弧或等弧所对圆周角都相等。((22)半圆或直径所对的圆周角都等于)半圆或直径所对的圆周角都等于90°;90°;反之,也成立。反之,也成立。例.如图OA、OB、OC都是⊙O的半径,∠AOB=2∠BOC.求证:∠ABC=∠BAC.CBOA例.已知:△ABC的三个顶点在⊙O上,∠BAC=50°,∠ABC=47°,求∠AOB.解:有题意知:∠A、∠B、∠C是圆周角,∠AOB是圆心角.又∵∠BAC=50°,∠ABC=47°∴∠ACB=180°-(∠A+∠B)=180°-(50°+47°)=83°.∴∠AOB=2∠ACB=2×83°=166°.BACOAOBACB21又思考与巩固1.如图,在⊙O中,BOC=50°,∠求∠A的大小.●OBAC2.试找出下图中所有相等的圆周角.567812433、在圆中,一条弧所对的圆心角和圆周角分别为(2x+100)°和(5x—30)°,求这条弧所对的圆心角和圆周角的度数。4、如图,∠A是圆O的圆周角,∠A=40°,求∠OBC的度数。OCBA(1)如图,已知圆心角∠AOB=100°,求圆周角∠ACB、∠ADB的度数?(2)一条弦分圆为1:4两部分,求这弦所对的圆周角的度数?DAOCB巩固练习: