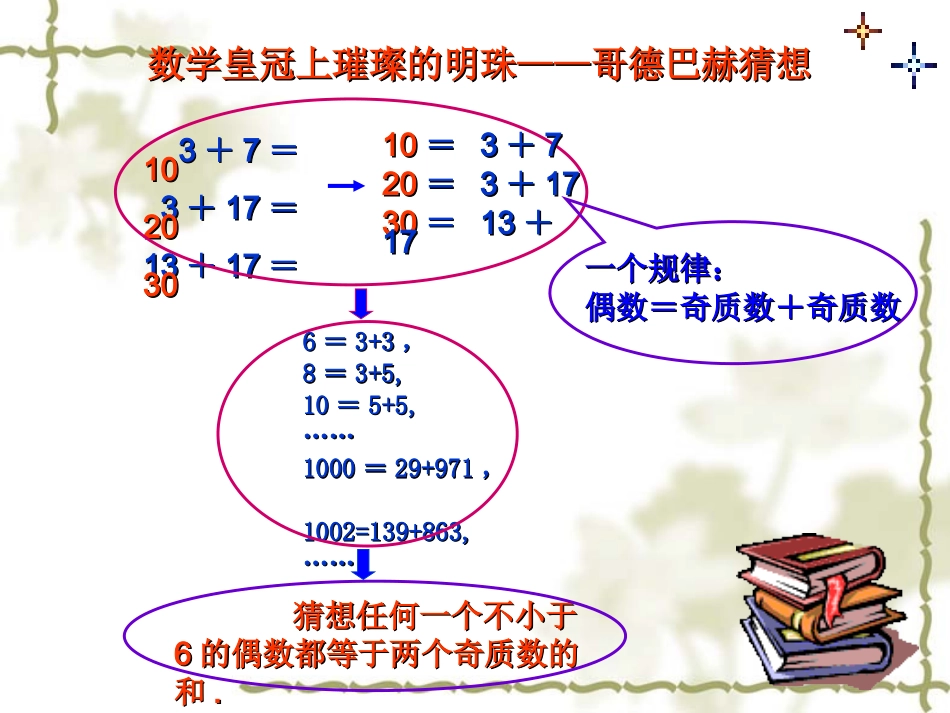
33++77==101033++1717==20201313++1717==30301010==33++772020==33++17173030==1313++171766==3+33+3,,88==3+5,3+5,1010==5+5,5+5,…………10001000==29+97129+971,,1002=139+863,1002=139+863,…………猜想任何一个不小于猜想任何一个不小于66的偶数都等于两个奇质数的的偶数都等于两个奇质数的和和..数学皇冠上璀璨的明珠数学皇冠上璀璨的明珠————哥德巴赫猜想哥德巴赫猜想一个规律:一个规律:偶数=奇质数+奇质数偶数=奇质数+奇质数费马猜想:法国业余数学家之王—费马(1601-1665)在1640年通对,,,,的观察,发现其结果都是素数,于是提出猜想:对所有的自然数,任何形如的数都是素数.后来瑞士数学家欧拉,发现不是素数,推翻费马猜想.020213F121215F2222117F32321257F4242165537F5252142949672976416700417F四色猜想:1852年,毕业于英国伦敦大学的弗南西斯.格思里来到一家科研单位搞地图着色工作时,发现了一种有趣的现象:“每幅地图都可以用四种颜色着色,使得有共同边界的国家着上不同的颜色.”,四色猜想成了世界数学界关注的问题.1976年,美国数学家阿佩尔与哈肯在美国伊利诺斯大学的两台不同的电子计算机上,用1200个小时,作了100亿逻辑判断,完成证明.哥德巴赫猜想的过程:哥德巴赫猜想的过程:具体的材料具体的材料观察分析观察分析猜想出一般性的结论猜想出一般性的结论归纳推理的过程:归纳推理的过程:课前热身1、由铜、铁、铝、金、银能导电,能归纳出什么结论?2、由直角三角形、等腰三角形、等边三角形内角和180度,能归纳出什么结论?3、观察等式:1+3=4=22,1+3+5=9=32,1+3+5+7=16=42,1+3+5+7+9=25=52能得出怎样的结论?由某类事物的具有某些特由某类事物的具有某些特征征,,推出该类事物的都具有这些特征推出该类事物的都具有这些特征的推理的推理,,或者由概括出或者由概括出的推理的推理,,称为称为归纳推理归纳推理((简称归纳简称归纳).).部分对象部分对象全部对象全部对象个别事实个别事实一般结论一般结论11,,33,,55,,77,,……,由此你猜想出,由此你猜想出第第个数是个数是_______._______.这就是从这就是从部分到整体部分到整体,,从从个别到一般个别到一般的的归纳推归纳推理理..12nn成语“一叶知秋”统计初步中的用样本估计总体统计初步中的用样本估计总体通过从总体中抽取通过从总体中抽取部分对象部分对象进进行观测或试验,进而对行观测或试验,进而对整体整体做出推断做出推断..意思是从一片树叶的凋落,知意思是从一片树叶的凋落,知道秋道秋天将要来到天将要来到..比喻由比喻由细微的迹象细微的迹象看出看出整体整体形势形势的变化,由的变化,由部分部分推知推知全体全体...,,2,1na1aa,1a1a1nn1n1n项公式试归纳出这个数列的通且项的第已知数列例.,,.anann算出数列的前几项的递推公式我们先根据已知为此与序号之间的对应关系项的第是数列数列的通项公式表示的分析;1a,1n1时当解;3121121a,3n3时当;21111a,2n2时当.4131131a,4n4时当.n1a,.4,n这个数列的通项公式为由此猜想数项都等于相应序号的倒数列的前观察可得.,.,1一种方向提供们的研究想可以为我但这个猜有待严格的证明猜想是否正确还虽然猜想一个了关于数列通项公式的我们通过归纳得到中在例例例2.2.数一数图中的凸多面体的面数数一数图中的凸多面体的面数FF、顶点数、顶点数VV和棱数和棱数E,E,然然后探求面数后探求面数FF、顶点数、顶点数VV和棱数和棱数EE之间的关系之间的关系..四棱柱四棱柱三棱锥三棱锥八面体八面体三棱柱三棱柱四棱锥四棱锥尖顶塔尖顶塔凸多面体凸多面体面数(面数(FF))顶点数顶点数((VV))棱数(棱数(EE))四棱柱四棱柱三棱锥三棱锥八面体八面体三棱柱三棱柱四棱锥四棱锥尖顶塔尖顶塔凸多面体凸多面体面数(面数(FF))顶点数顶点数((VV))棱数(棱数(EE))四棱柱四棱柱三棱锥三棱锥八面体八面体三棱柱三棱柱四棱锥四棱锥尖顶塔尖顶塔四棱柱四棱柱66881212凸多面体面数(F)...