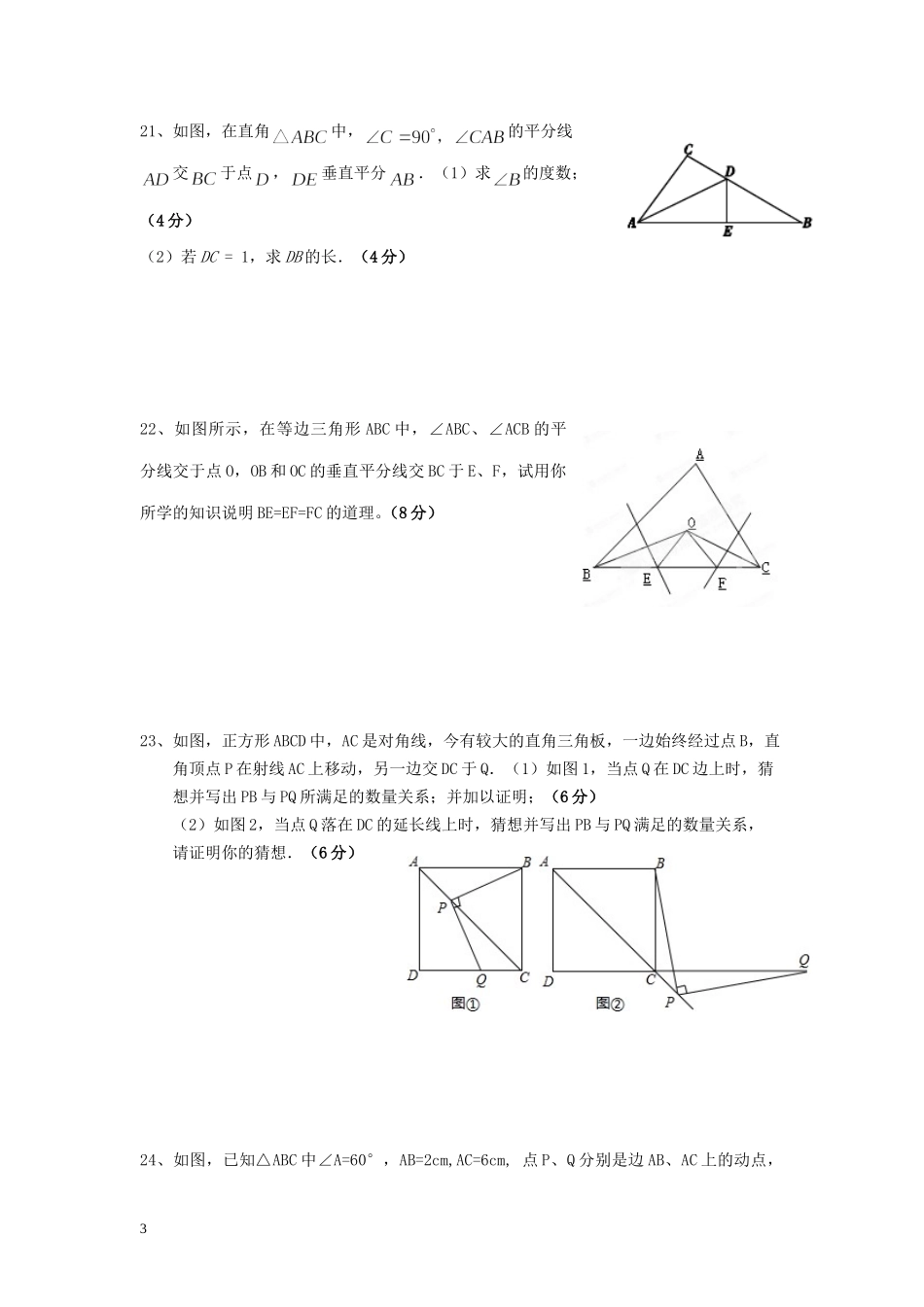
八上几何第三章测试题2一、选择题:(3×12=36分)1、如图1,∠B、∠C的平分线相交于F,过点F作DE∥BC,交AB于D,交AC于E,那么下列结论正确的是()①△BDF、△CEF都是等腰三角形;②DE=BD+CE;③△ADE的周长为AB+AC;④BD=CE;A.③④B.①②C.①②③D.②③④2、△ABC中,AB=AC,BC=5cm,作AB的垂直平分线交另一腰AC于D,连BD如果△BCD的周长是17cm,则腰长为()A.12cmB.6cmC.7cmD.5cm3、已知,如图2,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.恒成立的有______________(填序号).4、△ABC≌△DEF,AB=2,AC=4,若△DEF的周长为偶数,则EF的取值为()A.3B.4C.5D.3或4或55、如图,下列图案是几家银行的标志,其中是轴对称图形的有()A.1个B.2个C.3个D.4个6、平面内点A(-1,2)和点B(-1,-2)的对称轴是()A.x轴B.y轴C.直线y=4D.直线x=-17、如图,△ABN≌△ACM,AB=AC,BN=CM,∠B=50°,∠ANC=120°,则∠MAC的度数等于()A.120°B.70°C.60°D.50°.8、在直角三角形ABC中,∠ACB=90°,CD是斜边AB上的中线,且BC=CD.则∠B=()A、30°B、45°C、60°D、90°9、如图,把长方形沿对折后使两部分重合,若=110°,则∠1=()A.30°B.35C.40D.50°10、三角形内有一点到三角形三顶点的距离相等,则这点一定是三角形的()A、三条中线的交点;B、三边垂直平分线的交点;C、三条高的交战;D、三条角平分线的交点;11、如图所示,是四边形ABCD的对称轴,AD∥BC,现给出下列结论:①AB∥CD;②AB=BC;③AB⊥BC;④AO=OC其中正确的结论有()A、1个B、2个C、3个D、4个1ADBCEF(第1题图)ABCEDOPQ图2lOCBDAADOCB12如图,正方形ABCD的面积为12,ABE△是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PDPE的和最小,则这个最小值为()A.23B.26C.3D.6二、填空题:(3×6=18分)13、等腰三角形的一边长是6,另一边长是3,则周长为________________;14、等腰三角形的一内角等于50°,则其它两个内角各为;15、等腰三角形一腰上的高与另一腰上的夹角为30°,则顶角的度数为;16、一个汽车牌在水中的倒影为,则该车牌照号码____________.17、如图,已知的周长是21,OB,OC分别平分∠ABC和∠ACB,△ABC的面积是_______.18、已知三角形的的三个内角的度数之比为1:2:3,且最短边是3厘米,则最长边上的中线等于____________;三、解答题:(66分)19、如图,分别作点A(-3,0),B(-2,2)关于直线x=2的对称点A′、B′.(1)求A′、B′点坐标,(4分)(2)四边形ABB′A′的面积(4分)20、某中学八⑵班举行文艺晚会,桌子摆成两直条(如图中的AO,BO),AO桌面上摆满了桔子,OB桌面上摆满了糖果,站在C处的学生小明先拿桔子再拿糖果,然后到D处座位上,请你帮助他设计一条行走路线,使其所走的总路程最短?(8分)2ADEPBC21、如图,在直角中,的平分线交于点,垂直平分.(1)求的度数;(4分)(2)若DC=1,求DB的长.(4分)22、如图所示,在等边三角形ABC中,∠ABC、∠ACB的平分线交于点O,OB和OC的垂直平分线交BC于E、F,试用你所学的知识说明BE=EF=FC的道理。(8分)23、如图,正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于Q.(1)如图1,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系;并加以证明;(6分)(2)如图2,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,请证明你的猜想.(6分)24、如图,已知△ABC中∠A=60°,AB=2cm,AC=6cm,点P、Q分别是边AB、AC上的动点,3ABCMNABCHMDAHBCMDBCAPQ点P从顶点A沿AB以1cm/s的速度向点B运动,同时点Q从顶点C沿CA以3cm/s的速度向点A运动,当点P到达点B时点P、Q都停止运动.设运动的时间为t秒.(1)(4分)当t为何值时AP=AQ;(2)(6分)是否存在某一时刻使得△APQ是直角三角形?若存在,求出t的值;若不存在,请说明理由.25、已知,M是等边△ABC边BC上的点.(...