任意角的三角函数__课件(用）VIP免费

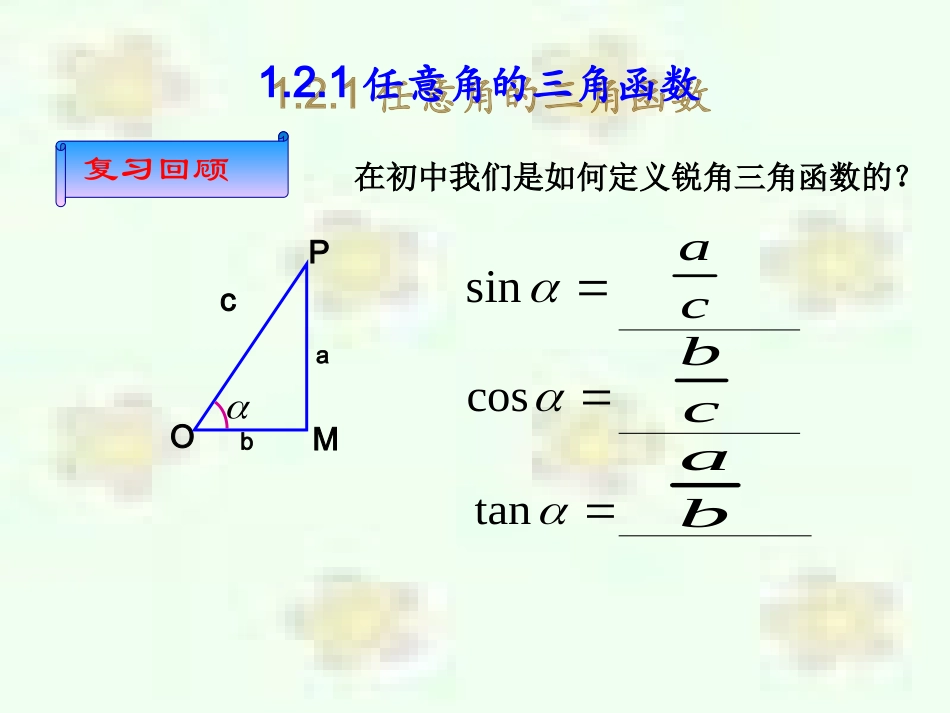
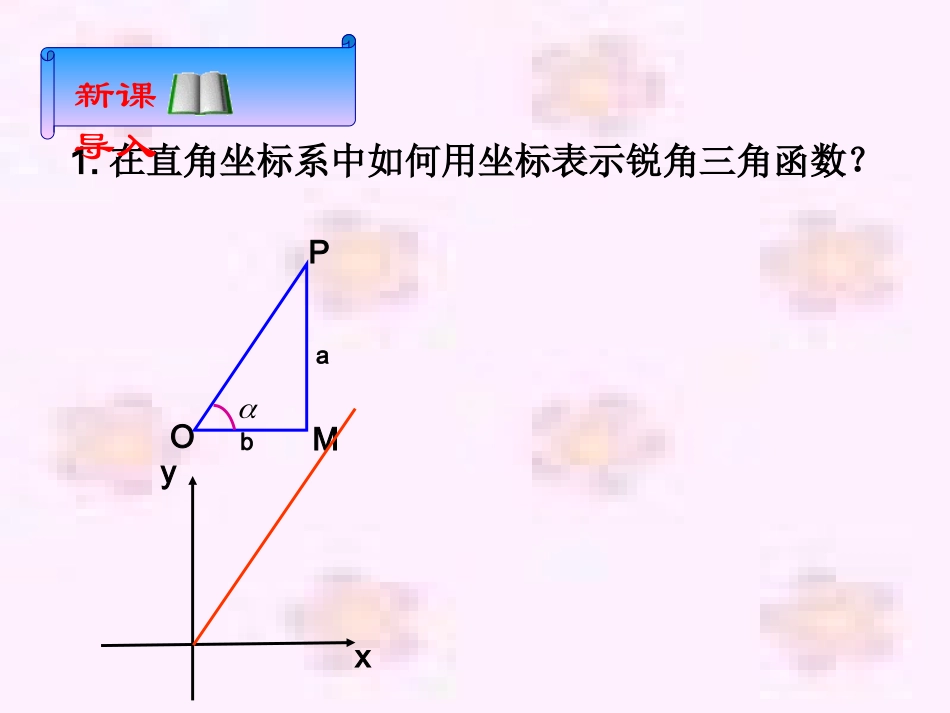
在初中我们是如何定义锐角三角函数的？sincostancacbba复习回顾OabMPc1.2.1任意角的三角函数1.2.1任意角的三角函数OabMPyx1.在直角坐标系中如何用坐标表示锐角三角函数？新课导入22:barOPbMPaOM其中yx1.在直角坐标系中如何用坐标表示锐角三角函数？raOPOMcosrbOPMPsinabOMMPtan新课导入﹒baP,﹒Mo如果改变点Ｐ在终边上的位置，这三个比值会改变吗？﹒PMOPMPsinOPOMcosOMMPtanOMP∽PMOPOPMPOOMMOPM诱思探究MOyxP(a,b)OPMPsinOPOMcosOMMPtanMOYXP(a,b)，则若1rOPbaab2.用单位圆定义任意角的三角函数)0,1(AxyoP),(yx的终边设是一个任意角，它的终边与单位圆交于一点),(yxp，那么（１）ysinxy叫做的正切，记作tan，即（３）)0(tanxxy（２）xcosx叫做cos，即的余弦，记作y叫做的正弦，记作sin，即正弦、余弦、正切都是以角为自变量，以单位圆上的点的坐或坐标的比值为函数值的函数，我们将它们统称为三角函数.标)0,1(AxyoP),(yx的终边说明（1）正弦就是交点的纵坐标，余弦就是交点横坐标的比值.的横坐标，正切就是交点的纵坐标与（3）由于角的集合与实数集之间可以建立一一对应关系，三角函数可以看成是自变量为实数的函数..（2）正弦、余弦总有意义.当的终边在y横坐标等于0，xytan无意义，此时)(2zkk轴上时，点P的例1求的正弦、余弦和正切值.3535AOB解：在直角坐标系中，作AOB，易知的终边与单位圆的交点坐标为)23,21(所以2335sin2135cos335tan，，实例剖析xyo﹒﹒AB35设角是一个任意角，是终边上的任意一点，点与原点的距离),(yxP022yxrP那么①叫做的正弦，即ryrysin②叫做的余弦，即rxrxcos③叫做的正弦，即xy0tanxxy任意角的三角函数值仅与有关，而与点在角的终边上的位置无关.P定义推广：).0(tan,cos,sin2222xxyyxxyxy例2已知角的终边经过点，求角的正弦、余弦和正切值.)4,3(0P5)4()3(220OP解:由已知可得设角的终边与单位圆交于，),(yxP分别过点、作轴的垂线、0PMPP00PMx400PM于是，;54||1sin000OPPMOPMPyyyMP30OMxOMOMP∽00POM;531cos00OPOMOPOMxx34cossintanxy4,30P0MOyxMyxP,135122222yxr135sinry1312cosrx125tanxy于是，巩固提高练习已知角的终边过点，求的三个三角函数值.5,12P解：由已知可得：探究：三角函数定义域sincostanRRZkk,21.三角函数的定义域ryasinrxacosxyatan()()()()()()()()()()()（）++--++--++--2.三角函数值在各象限的符号例3求证：当且仅当下列不等式组成立时，角为第三象限角.0tan0sin①②证明：因为①式成立,所以角的终边可能位于第三或第四象限，也可能位于y轴的非正半轴上；0sin又因为②式成立，所以角的终边可能位于第一或第三象限.0tan因为①②式都成立，所以角的终边只能位于第三象限.于是角为第三象限角.反过来请同学们自己证明.如果两个角的终边相同，那么这两个角的同一三角函数值有何关系？终边相同的角的同一三角函数值相等（公式一）tan)2tan(cos)2cos(sin)2sin(kkk其中zk利用公式一，可以把求任意角的三角函数值，转化为求角的三角函数值.360020到或到？例4确定下列三角函数值的符号：（1）（2）（3）解：250cos)672tan(4sin（1）因为是第三象限角，所以；2500250cos（2）因为=，而是第一象限角，所以；)672tan(48tan)360248tan(0)672tan(48练习确定下列三角函数值的符号516cos)34sin()817tan(（3）因为是第四象限角，所以.404sin例5求下列三角函数值：（1）（2）49cos)611tan(...