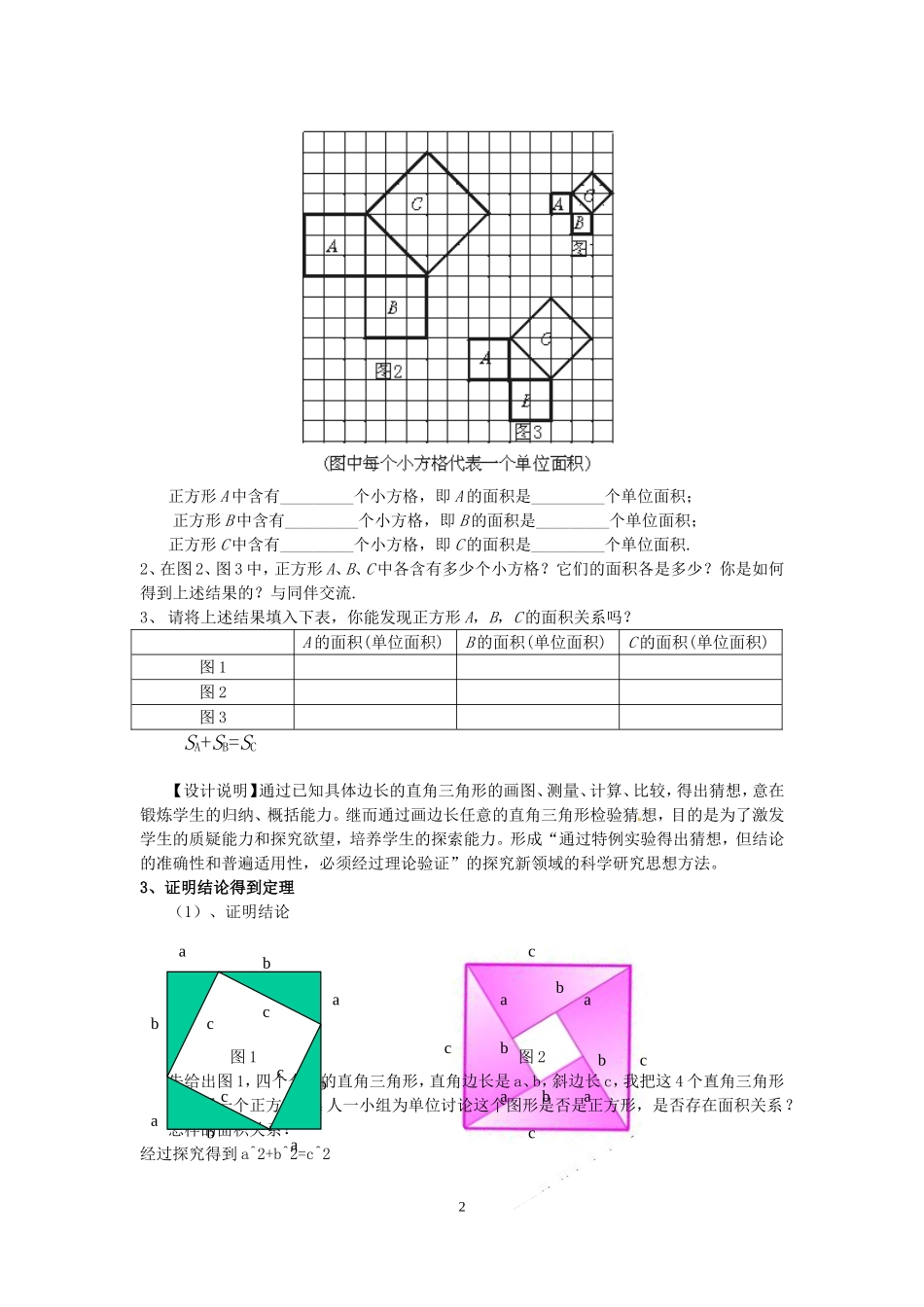
1.1探索勾股定理(1)一、教材地位和作用勾股定理是几何中几个重要定理之一,它揭示的是直角三角形中三边的数量关系。是七年级知识的自然发展和上升,也是今后学习实数、三角函数、向量等后续知识的基础。它在数学的发展中起过重要的作用,在现时世界中也有着广泛的应用。学生通过对勾股定理的学习,可以在原有的基础上对直角三角形有进一步的认识和理解。二、学情分析八年级学生已经具备一定的观察、归纳、探索和推理的能力.在小学,他们已学习了一些几何图形面积的计算方法(包括割补法),但运用面积法和割补思想解决问题的意识和能力还远远不够.部分学生听说过“勾三股四弦五”,但并没有真正认识什么是“勾股定理”.此外,学生普遍学习积极性较高,探究意识较强,课堂活动参与较主动,但合作交流能力和探究能力有待加强.三、教学目标:知识技能:1、经历探索、验证勾股定理的过程,发展推理能力。2、理解掌握勾股定理,会用勾股定理解决实际问题。过程方法:以教师为主导、学生为主体的学习方式,让学生经历动手操作、实验观察、归纳猜想、验证发现勾股定理的过程,培养学生探索能力,发展学生数形结合的数学思想方法。情感态度:1、通过引导学生动手操作观察发现、大胆猜想、自主探究、合作交流,使学生在合作中体验到数学活动充满了探索欲创造,使学生获得成功的体验,增强自信心,提高学习数学的兴趣。2、培养学生的爱国主义精神。四、教学重点与难点重点:探索勾股定理,并用它解决简单的实际问题。难点:探究活动二中正方形C的面积计算.五、教学准备学生:每一合作小组课前制作四个全等的直角三角形硬纸片。教师:制作多媒体课件和准备边长1厘米的方格纸(全班每人一张)六、教学过程1、创设情境导入新课一棵大树在一次强烈台风中于离地面7米处折断倒下,树顶落在离树根24米处.大树在折断之前高多少?学生将实际问题转化成数学问题,即“已知直角三角形的两边,如何求第三边”的问题,学生感到困难,教师指出学习今天的知识就能解决。【设计说明】数学来源于生活,学习勾股定理为了解决实际问题,意在激发学生的求知欲望。2、动手探索发现定理[来源:学科网ZXXK]1、观察下图,并回答问题:1aaaabbbbcccc正方形A中含有_________个小方格,即A的面积是_________个单位面积;正方形B中含有_________个小方格,即B的面积是_________个单位面积;正方形C中含有_________个小方格,即C的面积是_________个单位面积.2、在图2、图3中,正方形A、B、C中各含有多少个小方格?它们的面积各是多少?你是如何得到上述结果的?与同伴交流.3、请将上述结果填入下表,你能发现正方形A,B,C的面积关系吗?A的面积(单位面积)B的面积(单位面积)C的面积(单位面积)图1图2图3SA+SB=SC【设计说明】通过已知具体边长的直角三角形的画图、测量、计算、比较,得出猜想,意在锻炼学生的归纳、概括能力。继而通过画边长任意的直角三角形检验猜想,目的是为了激发学生的质疑能力和探究欲望,培养学生的探索能力。形成“通过特例实验得出猜想,但结论的准确性和普遍适用性,必须经过理论验证”的探究新领域的科学研究思想方法。3、证明结论得到定理(1)、证明结论图1图2先给出图1,四个全等的直角三角形,直角边长是a、b,斜边长c,我把这4个直角三角形围成了一个正方形。4人一小组为单位讨论这个图形是否是正方形,是否存在面积关系?怎样的面积关系?经过探究得到a^2+b^2=c^22aabbaabbcccc设计意图:通过4个全等的直角三角形围成一个四边形,判断是否是正方形,回顾三角形全等知识及几何基础。与此同时,利用面积公式,化简得到a^2+b^2=c^2,引出勾股定理。在此之上,引出图2,用勾股定理,探究中间的小正方形的面积。设计意图:通过图1,我引导学生探索验证得到了勾股定理。那么这4个全等的直角三角形围成了一个边长为c的正方形,利用刚得到的勾股定理探究中间小正方形的面积。由浅及深,运用新知。这个环节是本节课的重点,我将运用实际的直角三角形进行围正方形进行建构,分小组进行小组探讨合作交流,争取突破重难点。4、例题示范应用定理例1、已知在△ABC中,∠C=Rt∠ABC,BC=a,AC=b,AB=C(1)若a...