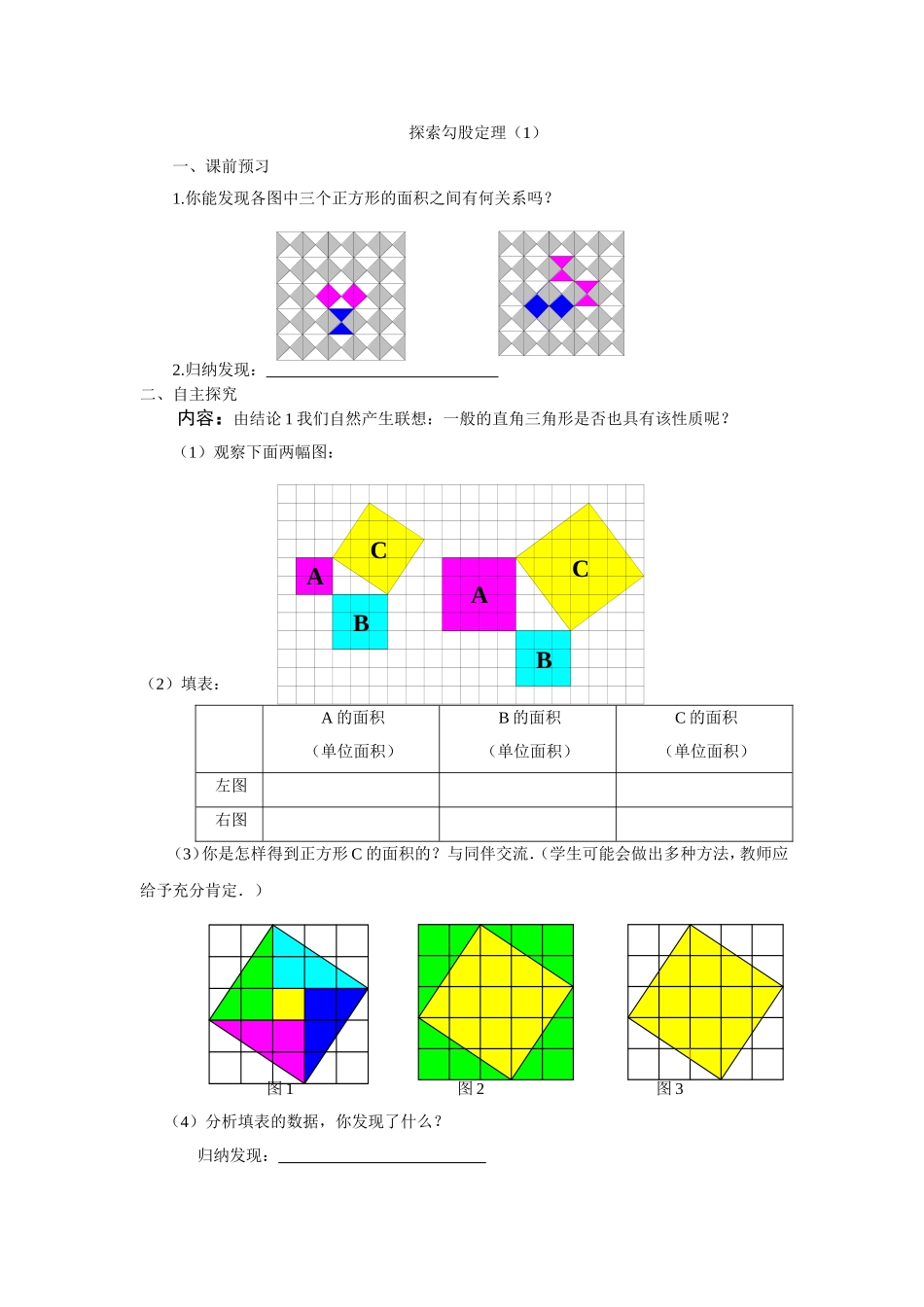
探索勾股定理(1)一、课前预习1.你能发现各图中三个正方形的面积之间有何关系吗?2.归纳发现:二、自主探究内容:由结论1我们自然产生联想:一般的直角三角形是否也具有该性质呢?(1)观察下面两幅图:(2)填表:A的面积(单位面积)B的面积(单位面积)C的面积(单位面积)左图右图(3)你是怎样得到正方形C的面积的?与同伴交流.(学生可能会做出多种方法,教师应给予充分肯定.)图1图2图3(4)分析填表的数据,你发现了什么?归纳发现:ABCCBA三、师生互动(1)你能用直角三角形的边长、、来表示上图中正方形的面积吗?(2)你能发现直角三角形三边长度之间存在什么关系吗?(3)分别以5厘米、12厘米为直角边作出一个直角三角形,并测量斜边的长度.刚才发现的规律对这个三角形仍然成立吗?(4)如果直角三角形两直角边长分别为、,斜边长为,那么三边之间的关系可以表示为;用文字语言可以概括为:(5)填空(阅读课本P4内容)在中国将此结论称为定理,在西方将此结论称为定理(6).求下列图形中未知正方形的面积或未知边的长度:四、拓展提高2.如图所示,一棵大树在一次强烈台风中于离地面10m处折断倒下,树顶落在离树根24m处.大树在折断之前高多少?五、达标测评1.解决课本P5的“随堂练习”2.在Rt△ABC中,∠C=90°,AC=5,BC=12,求AB的长。3.在Rt△ABC中,∠C=90°,AB=25,AC=20,求△ABC的面积。六、布置作业A层:1.为迎接新年的到来,同学们做了许多拉花布置教室,准备召开新年晚会,小刚搬来一?225100x1517CBA7cmDACB架高为2.5米的木梯,准备把拉花挂到2.4米的墙上,则梯脚与墙角的距离应为米.2.如图,小张为测量校园内池塘A,B两点的距离,他在池塘边选定一点C,使∠ABC=90°,并测得AC长26m,BC长24m,则A,B两点间的距离为m.B层:1.如图,阴影部分是一个半圆,则阴影部分的面积为.(不取近似值)2.底边长为16cm,底边上的高为6cm的等腰三角形的腰长为cm.C层:如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它恰好落在斜边AB上,且与AE重合,求CD的长.家庭作业:1.一艘轮船以16km/h的速度离开港口向东北方向航行,另一艘轮船同时离开港口以12km/h的速度向东南方向航行,它们离开港口半小时后相距km.2.如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面积的和是cm2.3.一个长为10m为梯子斜靠在墙上,梯子的顶端距地面的垂直高度为8m,梯子的顶端下滑2m后,底端滑动m.4.若直角三角形的两直角边之比为3:4,斜边长为20㎝,则斜边上的高为多少?257BACDE