勾股定理公开课VIP专享VIP免费

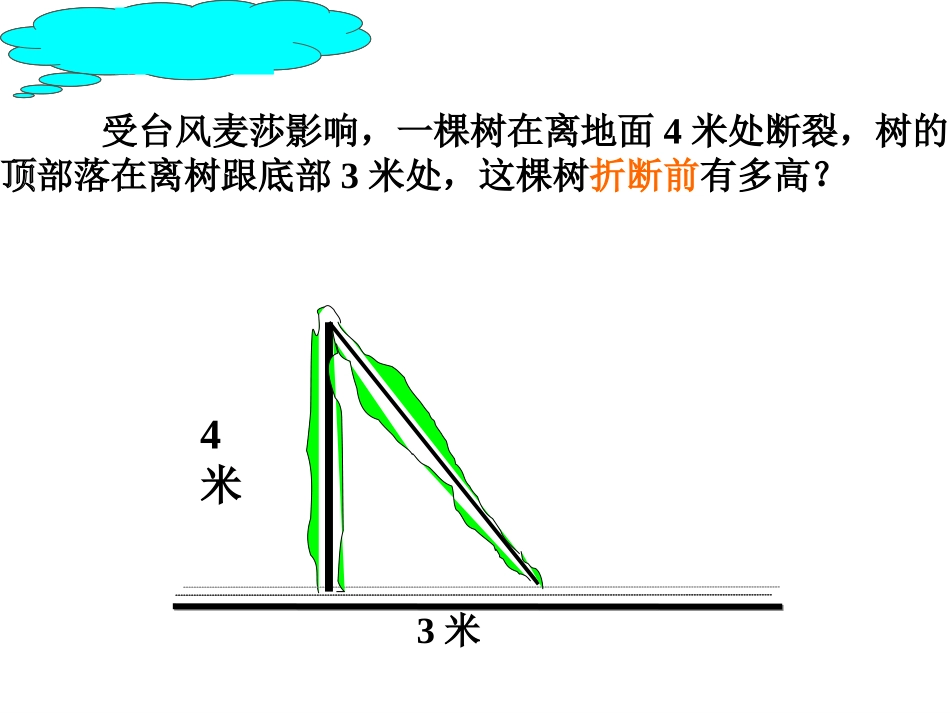
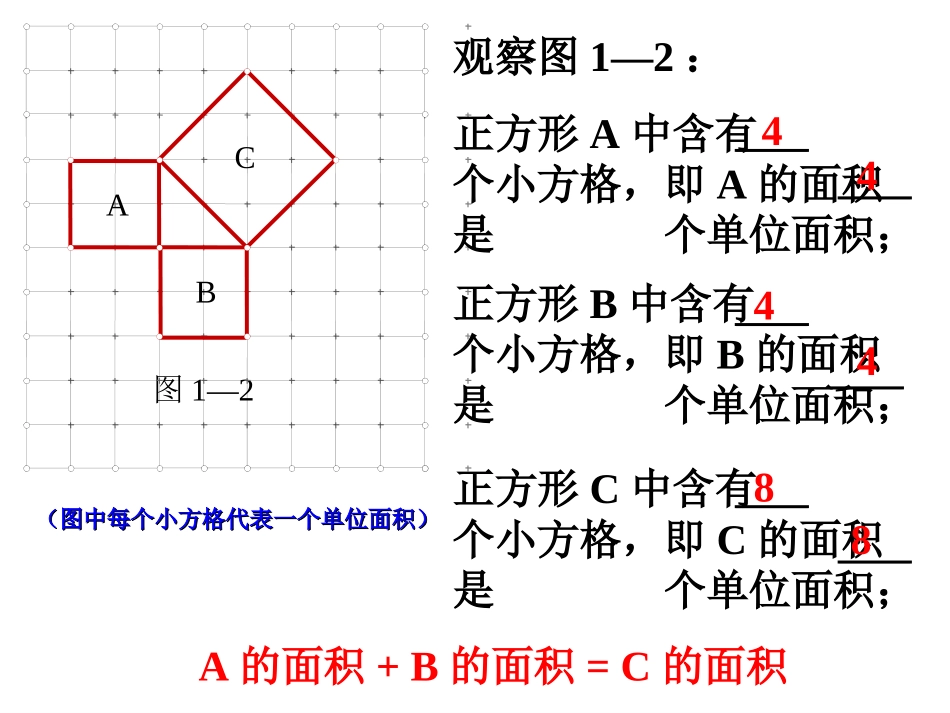
勾股定理受台风麦莎影响，一棵树在离地面4米处断裂，树的顶部落在离树跟底部3米处，这棵树折断前有多高？y=04米3米图1—2ABC观察图1—2：正方形A中含有个小方格，即A的面积是个单位面积；正方形B中含有个小方格，即B的面积是个单位面积；正方形C中含有个小方格，即C的面积是个单位面积；444488A的面积+B的面积=C的面积（图中每个小方格代表一个单位面积）（图中每个小方格代表一个单位面积）ABC（图中每个小方格代表一个单位面积）（图中每个小方格代表一个单位面积）观察左图正方形A中含有个小方格，即A的面积是个单位面积。正方形B的面积是个单位面积。正方形C的面积是个单位面积。999正方形C的面积怎样得到呢？123（2）（3）ABC（图中每个小方格代表一个单位面积）图2-1cS正方形1433182分“割”成四个直角边为整数的三角形（单位面积）ABC（图中每个小方格代表一个单位面积）图2-1cS正方形216218（单位面积）把C“补”成边长为6的正方形面积的一半ABC（图中每个小方格代表一个单位面积）图2-1（2）你能发现图中三个正方形A，B，C的面积之间有什么关系吗？SA+SB=SC对于等腰直角三角形有这样的性质：对于任意直角三角形都有这样的性质吗？两条直角边上的正方形面积之和等于斜边上的正方形的面积ABC你认为右图中的三个正方形之间还存在上述关系吗？与同伴进行交流。议一议ABC图3-1分割成若干个直角边为整数的三角形cS正方形25144312（面积单位）思考：面积A，B，C还有上述SA+SB=SC的关系吗？ABCacbSa+Sb=Sc观察所得到的各组数据，你有什么发现？猜想:两直角边a、b与斜边c之间的关系？a2+b2=c2每一个图中的三个正方形面积之间的关系是•勾股定理直角三角形两直角边的平方和，等于斜边的平方。•如果直角三角形的两直角边用a、b表示，斜边用c表示，那么勾股定理可表示为a2+b2=c2.•我国古代把直角三角形中较短的直角边称为勾，较长的直角边称为股，斜边称为弦。因此，我们称上述定理为勾股定理，国外称为毕达哥拉斯定理。在中国古代，人们把弯曲成直角的手臂的上半部分称为"勾"，下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”，较长的直角边称为“股”，斜边称为“弦”.勾股ABCacbccccabB1abC1FabD1GabA1EH图中的面积关系是：S正方形EFGH-4SABC△=S正方形A1B1C1D1由此，你能得出勾股定理的证明方法吗？已知：如图，在Rt△ABC中，∠C=90°，AB=c，BC=a，AC=b.求证：a2+b2=c2.证明取4个与Rt△ABC全等的直角三角形，把它们拼成如图所示的边长为a+b的正方形EFGH。可以证明四边形A1B1C1D1是边长为c的正方形（为什么？）。且S正方形EFGH-4SABC△=S正方形A1B1C1D121即(a+b)2-4×ab=c2.化简，得a2+b2=c2.操作:请同学们将手中的四个全等直角三角形拼成一个正方形，并观察图形间的面积关系3世纪我国汉代的赵爽指出：四个全等的直角三角形如下拼成一个中空的正方形，由大正方形的面积等于小正方形的面积与4个三角形的面积和得：两直角边的平方和等于斜边的平方赵爽弦图acbabcabab214)(2222cba思考：大正方形面积怎么求？赵爽弦图所以：大正方形的面积可以表示为，又可表示为。2c22214)(cabab22222cabaabb结论：结论变形直角三角形中，两直角边的平方和等于斜边的平方；abcc2=a2+b2y=01、如图，受台风麦莎影响，一棵树在离地面4米处断裂，树的顶部落在离树跟底部3米处，这棵树折断前有多高？应用知识回归生活4米3米1.在Rt△ABC中，∠C=90°，AB=c，BC=a，AC=b.(1)a=6，b=8，求c；(2)a=8，c=17，求b.2.在Rt△ABC中，AB=c，BC=a，AC=b，∠B=90°，a=3，b=4，求c.3.在直角三角形中，已知两边的长为3和4，求第三边的长.勾股定理的最大作用就是用在计算上，请同学们用勾股定理来解答下列各题：运用勾股定理时应注意：⑴在直角三角形中，认准直角边和斜边；⑵两直角边的平方和等于斜边的平方。11这节课你学到了什么知识？这节课你学到了什么知识？小结：小结：33、你还有什么疑惑或没有弄懂的地方？、你还有什么疑惑或没有弄懂的地方？22运用“运用“勾股定理”应注意什么问题？”应注意什么问题？美国第二十任总统伽...