分式的乘除运算VIP免费

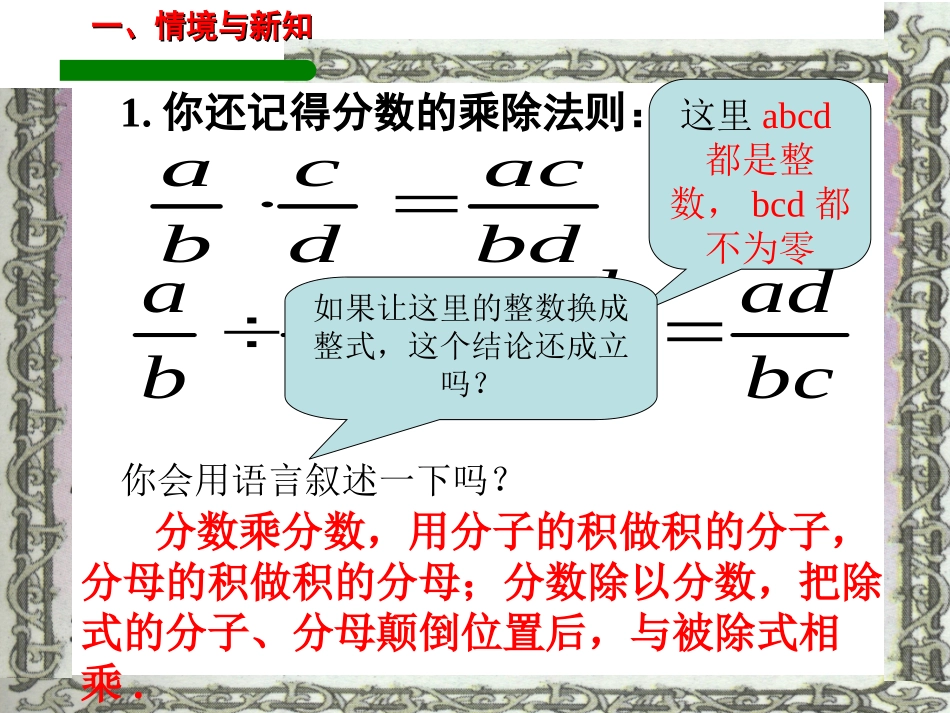
课首课首一个人的成就大小和一个人的努力程度成正比。知识的海洋里，需要你扬帆前行！一、情境与新知一、情境与新知1.你还记得分数的乘除法则：分数乘分数，用分子的积做积的分子，分母的积做积的分母；分数除以分数，把除式的分子、分母颠倒位置后，与被除式相乘.bdacdcbabcadcdbadcba你会用语言叙述一下吗？这里abcd都是整数，bcd都不为零如果让这里的整数换成整式，这个结论还成立吗？答：成立bdacdcbabcadcdbadcba这里abcd都是整式，bcd都不为零你会用语言叙述一下吗？分式乘分式，用分子的积做积的分子，分母的积做积的分母；分式除以分式：把除式的分子、分母颠倒位置后，与被除式相乘.二、新知的学习：分式的乘除法运算法则三、学以致用学数学是为了用数学解决问题，看看你会用了吗？（1）你会利用分式的乘除法运算法则计算下列各式吗？2222(1)axaybybx222222(2)axyayzbzbx22223(3)24ababccd222934xxxx4注意：计算结果要化为最简分式或整式补充计算（1）233344222aaaaaa)2)(1()3()3)(1()2)(2(:aaaaaaa原式解)2)(1)(3)(1()3)(2)(2(aaaaaaa122aaxxxxxxx36)3(446222)3()2)(3(31)2()3(2:2xxxxxx原式解22x补充计算（2）想一想,做一做☞☞2(1)nnnmmmnnmm22nm3(2)nnnnmmmmnnnmmm33nm(3)knnnnmmmm……kknmk个k为正整数归纳：分式的乘方法则：分式的乘方是把分式的分子、分母各自乘方，再把所得的幂相除。公式表示为：()kkknnmm(k为正整数)看看你会用上面的公式吗？计算：332)2)(1(cba2333(2):()abc解原式9368cba9368cba32333()abc32=43222)()())(2(xyxyyx443624)(:yxxyyx原式解464243xyxyyx5x3224234:[]yxyyxx2（）解原式课上练习：1、2、3作业:习题17.21.5.补充作业:计算42222222(1)(2)229(3)369xyababababababaaaa