任意角的三角函数课件(一)_第一课时VIP免费

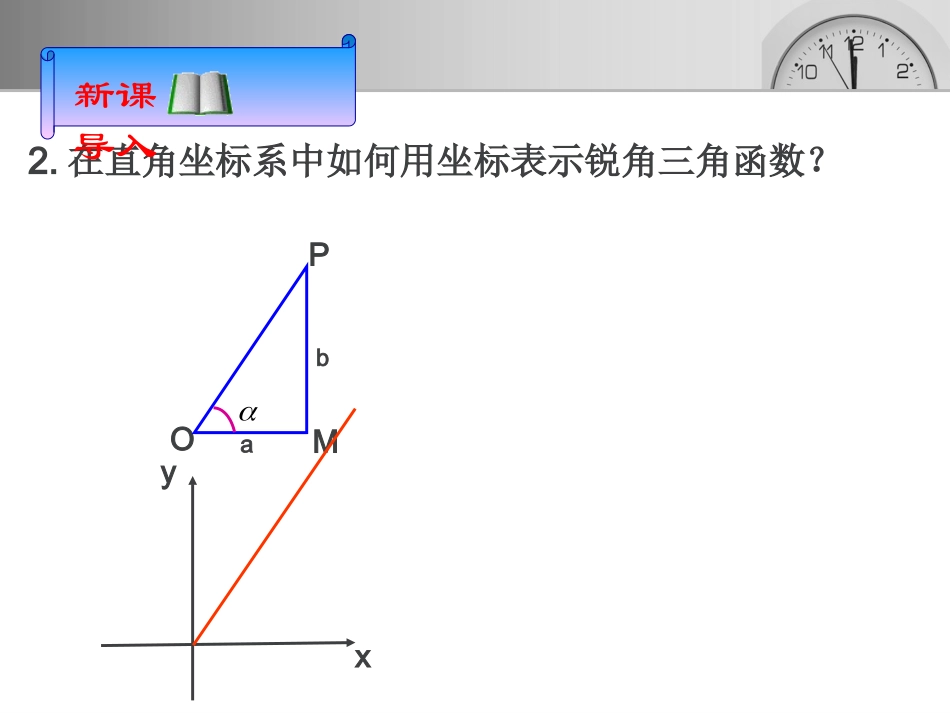
1、在初中我们是如何定义锐角三角函数的？sincostancbcaab复习回顾ObaMPc1.2.1任意角的三角函数1.2.1任意角的三角函数ObaMPyx2.在直角坐标系中如何用坐标表示锐角三角函数？新课导入22:barOPbMPaOM其中2.在直角坐标系中如何用坐标表示锐角三角函数？raOPOMcosrbOPMPsinabOMMPtan新课导入如果改变点Ｐ在终边上的位置，这三个比值会改变吗？﹒PMOPMPsinOPOMcosOMMPtanOMP∽PMOPOPMPOOMMOPM诱思探究MOyxP(a,b)OPMPsinOPOMcosOMMPtan221barOPbaab3.锐角三角函数（在单位圆中）以原点O为圆心，以单位长度为半径的圆叫单位圆y1oP),(baxMM4.用单位圆定义任意角的三角函数)0,1(AxyoP),(yx的终边设是一个任意角，它的终边与单位圆交于一点),(yxp，那么（１）ysinxy叫做的正切，记作tan，即（３）)0(tanxxy（２）xcosx叫做cos，即的余弦，记作y叫做的正弦，记作sin，即正弦、余弦、正切都是以角为自变量，以单位圆上的点的坐标或坐标的比值为函数值的函数，我们将它们统称为三角函数.例1求的正弦、余弦和正切值.3535AOB解：在直角坐标系中，作AOB，易知的终边与单位圆的交点坐标为)23,21(所以2335sin2135cos335tan，，实例剖析xyo﹒﹒AB35练习1：P15第1题练习2：求角的三个三角函数值练习1：P15第1题练习2：求角的三个三角函数值例2：如图已知角α的终边上一点是求角α的正弦、余弦和正切值。解：根据任意角的三角函数定义：23sin21cos3tanOxy)23,21(P若已知角α的终边一点的坐标，则先判断点是否在单位圆上，若是则直接利用定义求三角函数值。若不是呢，如何求？例如P为时请大家课后讨论。实例剖析MM(3,4)点评：点评：13(,)22p角α0°90°180°270°360°30°45°60°弧度数0sinα010－10cosα10－101tanα0不存在0不存在0练习３、P15第3题练习３、P15第3题223264321233322222321311探究：请根据任意角的三角函数定义,思考（1）正弦、余弦和正切函数的定义域；（2）这三种函数的值在各个象限的符号；填入课本P13的表格中；例3．求证：当且仅当不等式组成立时，角为第三象限角.0tan0sin探究：根据三角函数的定义,终边相同的角的同一三角函数值有和关系?终边相同的角的同一三角函数值相等.即有公式一sin(2)sinkcos(2)cosktan(2)tankkZ例4.确定下列三角函数值的符号cos250sin()4tan(672)tan3例5.求下列三角函数值'sin1480109cos411tan()6小结:1.任意角的三角函数是由角的终边与单位圆交点的坐标来定义的.2.三角函数值的符号是利用三角函数的定义来推导的.要正确记忆三个三角函数在各个象限内的符号；3.诱导公式一的作用可以把大角的三角函数化为小角的三角函数.归纳总结课本第20页习题1.2A组3、4题.《同步导练》课后作业