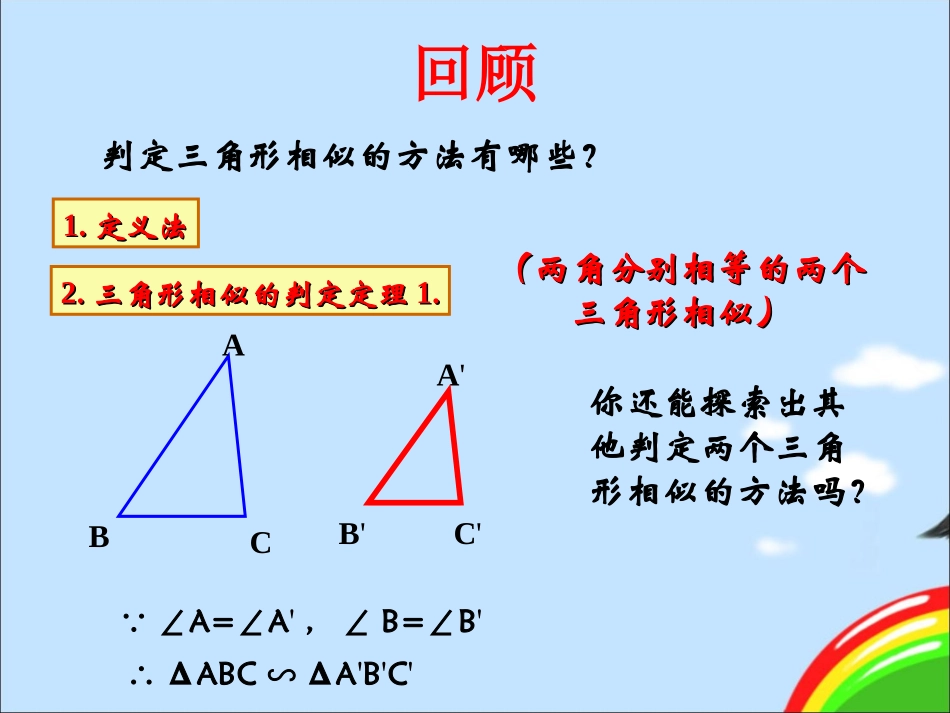
4.4.2探索三角形相似的条件(二)判定三角形相似的方法有哪些?2.2.三角形相似的判定定理三角形相似的判定定理1.1.ABCA'C'B'∵∠A=∠A',∠B=∠B'∴ΔABC∽ΔA'B'C'回顾你还能探索出其他判定两个三角形相似的方法吗?1.1.定义法定义法(两角分别相等的两个(两角分别相等的两个三角形相似)三角形相似)探索如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似吗?如果两个三角形有两边对应成比例,那么这两个三角形相似吗?如果再增加一个条件呢?你能类比全等三角形的判定定理思考吗?ABCC'B'A'6cm4cm3cm2cm两边对应成比例且夹角相等∠B=40°∠B'=40°画一画画一画同桌分工,画△ABC和△A,B,C,,使∠B=40°,∠B,=40°,AB=4cm,BC=6cm,A,B,=2cm,,B,C,=3cm,探究△ABC和△A,B,C,是否相似结论A'B'B'C'ABBC,∠B’=∠B,∵△A’B’C’∽△ABC∴几何表述:例1.判断图中△AEB和△FEC是否相似,并说明理由.练习1:课本P92随堂练习练习2:已知△ABC和△A’B’C’,根据下列条件判断它们是否相似.(2)∠B=∠B’=75°,∠C=50°,∠A’=55°(1)∠A=45°,AB=12cm,AC=15cm∠A’=45°,A’B’=16cm,A’C’=20cm注意:注意:两边对应成比例且其中一边所对的角对应相等的两个三角形不一定相似。注意:注意:两边对应成比例且其中一边所对的角对应相等的两个三角形不一定相似。观察上面图形,这两个三角形相似吗?议一议议一议例2(课本P91例1):如图,D、E分别是△ABC的边AC、AB上的点。AE=1.5,AC=2,BC=3,且,求DE的长。ADAB34AEDCB如图,D在△ABC的AB边上,AD=1,BD=2,AC=,问△ACD与△ABC相似吗?请说明你的理由.3DCBA两个三角形相似的判定方法:(1)定义法(2)两角对应相等的两个三角形相似.(3)两边对应成比例且夹角相等的两个三角形相似.看已知条件判定相似选方法找出判定方法中所需的条件☞☞课本P93习题4.6第2,3题