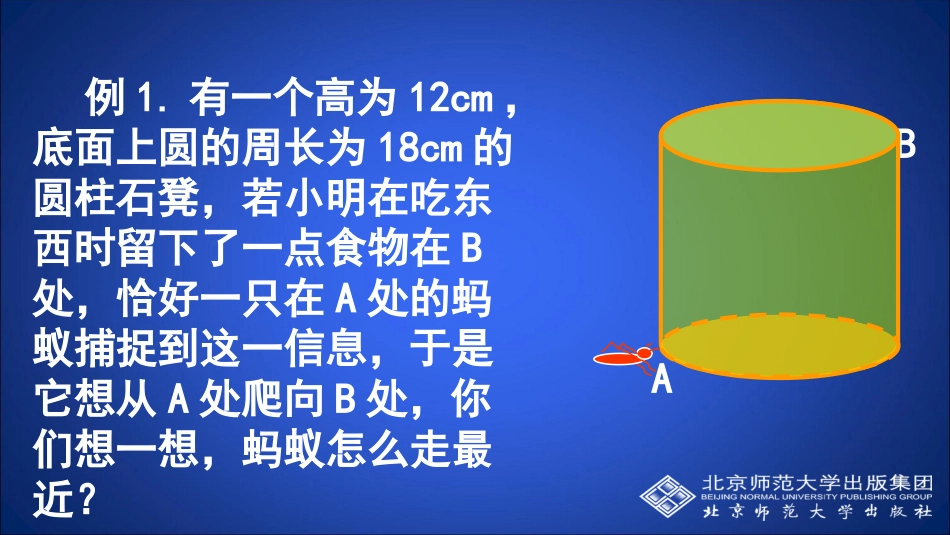
第一章勾股定理3.勾股定理的应用一、有关最短路径的问题BA例1.有一个高为12cm,底面上圆的周长为18cm的圆柱石凳,若小明在吃东西时留下了一点食物在B处,恰好一只在A处的蚂蚁捕捉到这一信息,于是它想从A处爬向B处,你们想一想,蚂蚁怎么走最近?以小组为单位,研究蚂蚁爬行的最短路线.合作探究BA蚂蚁A→B的路线BAA’dABA’ABBAO下一页>>ABA’BAA’rOh怎样计算AB?在Rt△AA’B中,利用勾股定理可得:222'ABAAAB侧面展开图例2.如图所示,长方体的高为3cm,底面是正方形,其边长是2cm,现在有一只蚂蚁从A处出发,沿着长方体的表面到达C处,求蚂蚁爬行的最短路线的长。CA3cm2cm1.如图,在棱长为10cm的正方体的一个顶点A处有一只蚂蚁,现要向顶点B处爬行,已知蚂蚁爬行的速度是1cm/s,且速度保持不变,问蚂蚁能否在20s内从A爬到B?B食物A举一反三AB举一反三1.如图,在棱长为10cm的正方体的一个顶点A处有一只蚂蚁,现要向顶点B处爬行,已知蚂蚁爬行的速度是1cm/s,且速度保持不变,问蚂蚁能否在20s内从A爬到B?二、有关楼梯问题ABC1.如图是一段楼梯,高BC是3m,斜边AC是5m,如果在楼梯上铺地毯,那么需要地毯的长是多少m?2.如图,台阶A处的蚂蚁要爬到B处搬运食物,它怎么走最近?并求出最近距离.3220BA222215206252525ABAB.解:答:沿AB走最近,最近距离为25.三、与方程结合问题1.在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面是一个边长为10尺的正方形,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?ABCDEF2.在长方形纸片ABCD中,AB=3cm,AD=9cm,将此长方形纸片折叠,使得点D与点B重合,折痕为EF,求△ABE的面积。交流小结