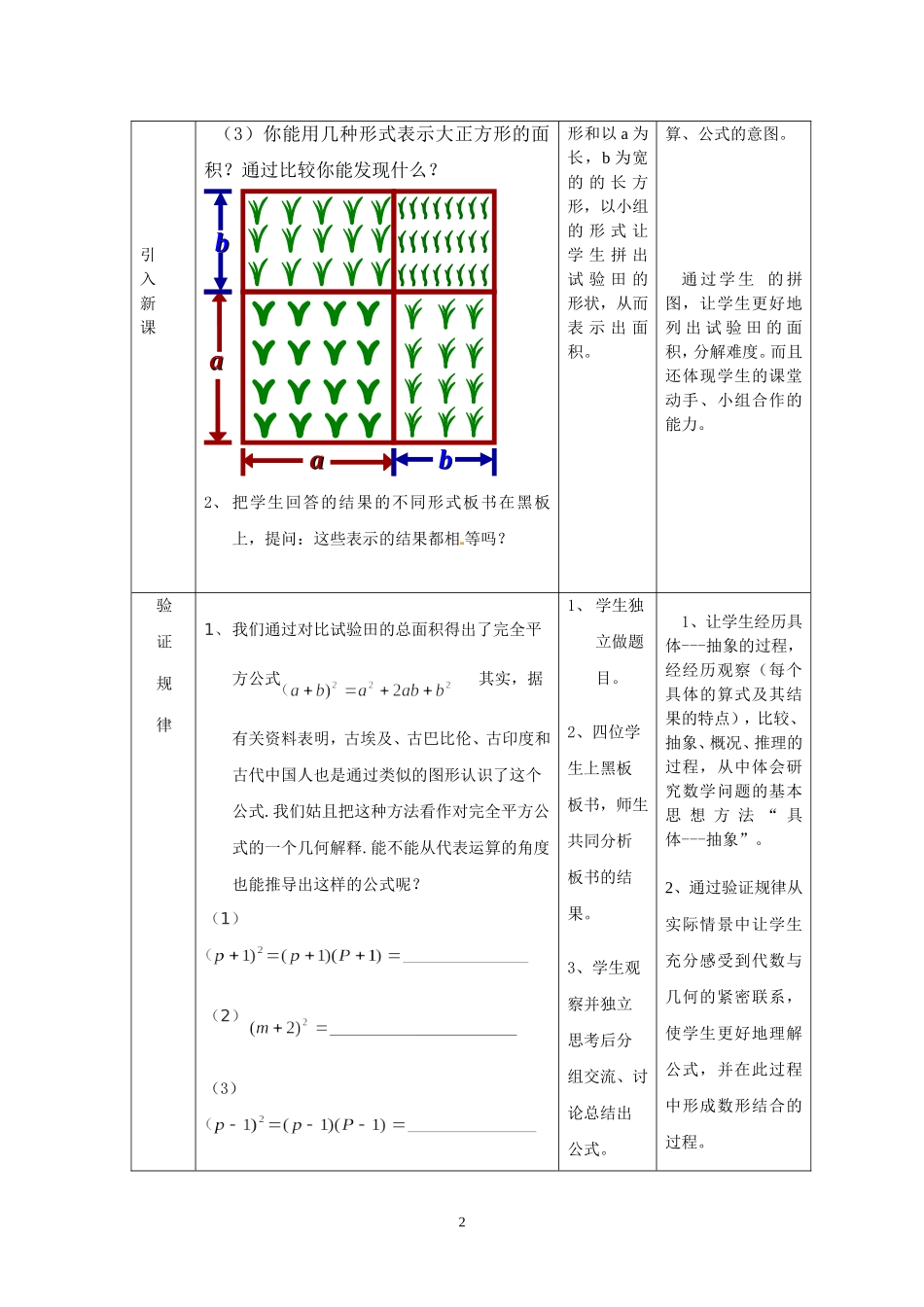
《完全平方公式》教学设计广州花都区花东镇北兴初级中学石榴林教学目标知识技能1、经历探索完全平方公式的过程,进一步发展推理能力。2、会推导完全平方公式,并能运用公式进行简单的计算。3、了解的几何背景。数学思考通过观察、猜想、类比可以获得数学猜想,体验数学活动充满着探索性和创造性,感受证明的必要性、证明过程的严谨性以及结论的确定性;解决问题通过猜想,验证以及运用完全平方公式,尝试从不同的角度寻求解决问题的方法。情感态度1、了解完全平方公式的几何背景,培养良好的学习情感.。2、通过交流、研讨活动,培养主动与他人合作的意识。重点1.完全平方公式的推导过程、结构特点、语言表述、几何解释;2.完全平方公式的应用.难点1、用公式的结构特征判断题目能否使用公式,以及运用公式进行简单运算.2、数学公式中字母的高度概括性、广泛应用性及换元思想的渗透。教学方法探究式、启发式、讨论式教学准备多媒体、课件。教学设计教学流程教师活动学生活动设计意图复习回顾用课件展示(1)、多项式与多项式相乘的法则(a+b)(m+n)=am+an+bm+bn.(2)、根据乘方的定义,我们知道:a2=a·a,那么应该写成什么样的形式呢?学生回答老师问题让学生在学习本节课之前做好知识回顾。创设问题情景1、如图,一块边长为a米的正方形实验田,因需要将其边长增加b米。问:(1)原实验田面积是(2)增加部分面积事先让学生准备好两个分别以a,b为边长的正方向学生提供源自于生活、几何的实际背景,让他们在比较试验田的面积当中猜想完全平方公式,突出用几何图形解析代数运1引入新课(3)你能用几种形式表示大正方形的面积?通过比较你能发现什么?2、把学生回答的结果的不同形式板书在黑板上,提问:这些表示的结果都相等吗?形和以a为长,b为宽的的长方形,以小组的形式让学生拼出试验田的形状,从而表示出面积。算、公式的意图。通过学生的拼图,让学生更好地列出试验田的面积,分解难度。而且还体现学生的课堂动手、小组合作的能力。验证规律1、我们通过对比试验田的总面积得出了完全平方公式其实,据有关资料表明,古埃及、古巴比伦、古印度和古代中国人也是通过类似的图形认识了这个公式.我们姑且把这种方法看作对完全平方公式的一个几何解释.能不能从代表运算的角度也能推导出这样的公式呢?(1)(2)(3)1、学生独立做题目。2、四位学生上黑板板书,师生共同分析板书的结果。3、学生观察并独立思考后分组交流、讨论总结出公式。1、让学生经历具体---抽象的过程,经经历观察(每个具体的算式及其结果的特点),比较、抽象、概况、推理的过程,从中体会研究数学问题的基本思想方法“具体---抽象”。2、通过验证规律从实际情景中让学生充分感受到代数与几何的紧密联系,使学生更好地理解公式,并在此过程中形成数形结合的过程。aaaabbbb2(4)通过计算,你发现什么规律?2、根据上面的规律你能直接写出下列式子的结果吗?_______________,总结公式引导得出完全平方公式:文字:两数和的平方,等于这两数的平方和,加上这两数乘积的2倍。公式:2、引导学生观察公式的左右边,进一步挖掘公式的结构特征:①公式左边是两项(数)的和的平方。②公式的右边有三项,两个平方项,且符号相同,一个两项乘积的两倍。结合两个公式的特征,可用一句顺口溜来强化记忆:“首平方,尾平方,首尾两倍中间放。”公式变形为:(首+尾)2=首2+2×首×尾+尾2的和,加上它们乘积的两倍;3、模仿练习:=1、学生在老师的引导下通过小组合作用自己的语言概括总结完全平方公式的语言描述和字母表示。2、小组运用顺口溜来应用。3、学生独立完成1、培养学生的小组合作能力。2、让学生经符号语言转化为文字语言,发展学生的数形语言表达能力.3、学生在用文字语言表述公式内容时,可以加深对公式结构特征的理解。4、。3=知识延伸换元拓展提问:2)(ba等于什么?可否利用上面的公式表示出来?通过讨论,尝试得到2222)(bababa5、提出问题,你能找出2222)(bababa这两个公式的共同点与区别吗?4、小组讨论出共同点与不同点。1、是为了加深学生对公式中字母a,b的广泛意义的理解,并...