第四章因式分解的复习课（4月30日周三上）VIP免费

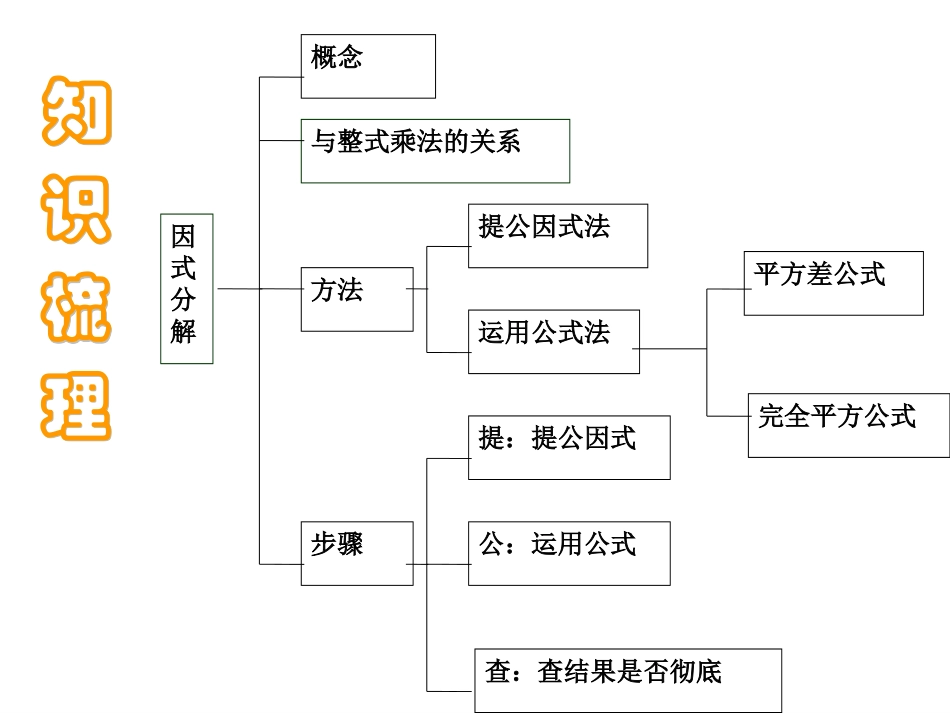
2014年4月30日周三上知识梳理知识梳理因式分解概念与整式乘法的关系方法提公因式法运用公式法平方差公式完全平方公式步骤提：提公因式公：运用公式查：查结果是否彻底整式乘法因式分解)(cbammambmc平方差公式a²-b²=(a+b)(a-b)完全平方公式a²±2ab+b²=(a±b)²把一个多项式化成几个整式的积的形式叫做因式分解，也叫分解因式。一个多项式中每一项都含有的相同的因式，叫做这个多项式各项的公因式。如果一个多项式的各项含有公因式，那么可以把公因式提取出来进行因式分解，这种因式分解的方法叫做提取公因式法。平方差公式法和完全平方公式法统称公式法平方差公式：适用于平方差形式的多项式完全平方公式法：适用于完全平方式。公式法因式分解基本概念提公因式法1.公因式确定（1）系数：取各系数的最大公约数；（2）字母：取各项相同的字母；（3）相同字母的指数：取最低指数。2.变形规律：（1）x-y=-(y-x)(2)-x-y=-(x+y)(3)(x-y)2=(y-x)2(4)(x-y)3=-(y-x)33.一般步骤（1）确定应提取的公因式；（2）多项式除以公因式，所得的商作为另一个因式；（3）把多项式写成这两个因式的积的形式。提公因式法：提公因式法：用平方差公式分解因式的关键：多项式是否能看成两个数的平方的差；用完全平方公式分解因式的关键：在于判断一个多项式是否为一个完全平方式；平方差公式：a2-b2=(a+b)(a-b)完全平方公式：a2+2ab+b2=(a+b)2a2-2ab+b2=(a-b)2公式法公式法因式分解的一般步骤：一提：先看多项式各项有无公因式，如有公因式则要先提取公因式；二套：再看有几项，如两项，则考虑用平方差公式；如三项，则考虑用完全平方公式；四查：最后用整式乘法检验一遍，并看各因式能否再分解，如能分解，应分解到不能再分解为止。三变：若以上两步都不行，则将考虑将多项式变形，使之能“提”或能“套”。[如(x+y)²-x-y=(x+y)(x+y-1）因式分解的应用2，若A·B=0，则A=0或B=01，运用因式分解进行多项式除法3,运用因式分解解简单的方程否否是A层练习下列代数式的变形当中哪些是因式分解，哪些不是？(1)3a2+6a=3a(a+2)(2)(2y+1)(2y-1)=4y2-1(3)18a3bc=3a2b·6ac是不是?是不是?是不是?基本概念(4)X²+2X+1=X(X+2)+1(5)a²+1=a(a+1/a).是不是?否是不是?否否是否是B层练习检验下列因式分解是否正确？(1)2ab2+8ab3=2ab2(1+4b)(2)2x2-9=(2x+3)(2x-3)(3)x2-2x-3=(x-3)(x+1)(4)36a2-12a-1=(6a-1)2答案答案答案答案基本概念C层练习填空1.若x2+mx-n能分解成(x-2)(x-5),则m=,n=。2．x2-8x+m=(x-4)(),且m=。-7-10x-416基本概念A层练习将下列各式分解因式：⑴-a²-ab；⑵m²-n²；⑶x²+2xy+y²(4)3am²-3an²；(5)3x³+6x²y+3xy²基本方法=-a(a+b)=(m+n)(m-n)=(x+y)²=3a(m+n)(m-n)=3x(x+y)²B层练习将下列各式分解因式：⑴18a²c-8b²c⑵m4-81n4⑶x²y²-4xy+4基本方法=2c(3a+2b)(3a-2b)=(m2+9n2)(m+3n)(m-3n)=（xy–2）²C层练习将下列各式分解因式：⑴(2a+b)²–(a–b)²；(2)(x+y)²-10(x+y)+25(3)4a²–3b(4a–3b)基本方法=(2a-3b)²=(x+y-5)²=3a(a+2b)简化计算(1)562+56×44(2)9992-9982变式若a=99,b=-1,则a2-2ab+b2=____________；基本应用解方程：x³-9x=0变式解下列方程：(3x-4)²-(3x+4)²=48基本应用例1:有关完全平方式的运用1.若9x2+mx+16是完全平方式,则m=.2.若x2-6xy+m,是完全平方式,则m=.3.若x2-x+m2,是完全平方式,则m=.4.若x2+25与一个单项式的和是一个完全平方式,则这个单项式可以是.例2:因式分解的应用1.简便计算(1)(2)5×102004-102005(3)9992-1002×998(4)19992-3994×1999+19972(5)20062-20052+20042-20032+…+22-122)436()413()201011)(200911()411)(311)(211).(6(222222.条件式计算(1)若2b-a=-3,ab=5,则2a2b-4ab2的值是.(2)若∣2x-y+5∣+(x+2y-4)2=0,则(2x-y)3-(x-3y)(y-2x)2的值是.(3)若(A+2005)2=987654321,则(A+2015)(A+1995)的值是.(4)若(a2+b2)(a2+b2-2)=-1,则a2+b2的值是.(5)若4a2+b2+4a-6b+10=0,则a3b-ab3的值是.例3:因式分解的应用例4:多项式除法1.(4x2-12xy+9y2)÷(3y-2x)2.(-a+9a3)÷(3a-1)3.[(x+3y)²-4x2]÷(x+y)练一练：A层练习...