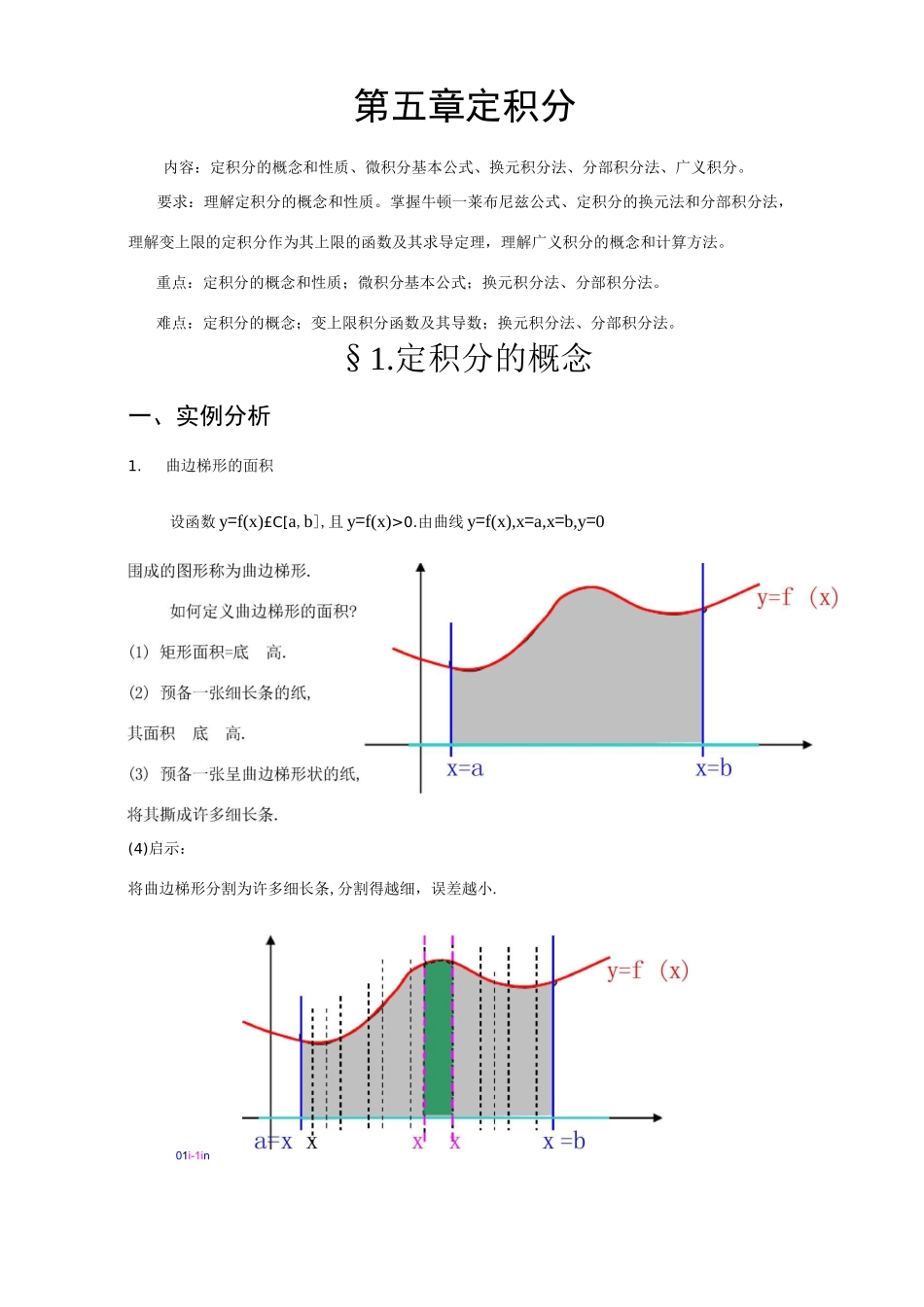
第五章定积分内容:定积分的概念和性质、微积分基本公式、换元积分法、分部积分法、广义积分。要求:理解定积分的概念和性质。掌握牛顿一莱布尼兹公式、定积分的换元法和分部积分法,理解变上限的定积分作为其上限的函数及其求导定理,理解广义积分的概念和计算方法。重点:定积分的概念和性质;微积分基本公式;换元积分法、分部积分法。难点:定积分的概念;变上限积分函数及其导数;换元积分法、分部积分法。§1.定积分的概念一、实例分析1.曲边梯形的面积设函数y=f(x)£C[a,b],且y=f(x)>0.由曲线y=f(x),x=a,x=b,y=0(4)启示:将曲边梯形分割为许多细长条,分割得越细,误差越小.01i-1in定义:S=lim九T0工f(g)Axiii=1(九=max第i个细长条面积AS沁f(g)Ax(V^G[x,x],Ax二x-x)iiiii-1iiii-1曲边梯形面积:SQ工f(g)Axiii=1定积分概念示意图.ppt抛开上述过程的几何意义,将其数学过程定义为定积分.二、定积分的定义1.定义设y=f(x)在[a,b]有定义,且有界.⑴分割:用分点a=x