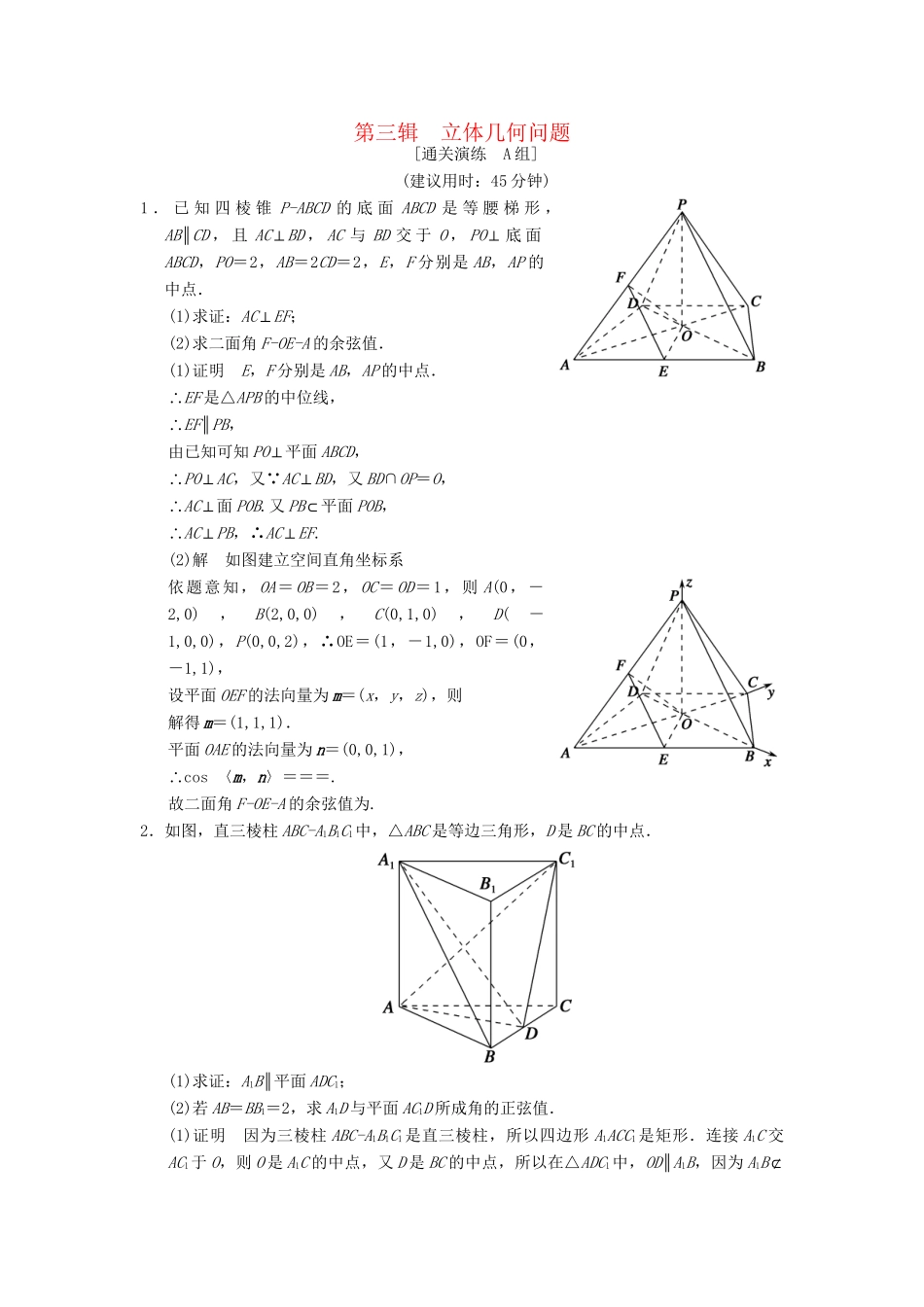
第三辑立体几何问题[通关演练A组](建议用时:45分钟)1.已知四棱锥P-ABCD的底面ABCD是等腰梯形,AB∥CD,且AC⊥BD,AC与BD交于O,PO⊥底面ABCD,PO=2,AB=2CD=2,E,F分别是AB,AP的中点.(1)求证:AC⊥EF;(2)求二面角F-OE-A的余弦值.(1)证明E,F分别是AB,AP的中点.∴EF是△APB的中位线,∴EF∥PB,由已知可知PO⊥平面ABCD,∴PO⊥AC,又 AC⊥BD,又BD∩OP=O,∴AC⊥面POB.又PB⊂平面POB,∴AC⊥PB,∴AC⊥EF.(2)解如图建立空间直角坐标系依题意知,OA=OB=2,OC=OD=1,则A(0,-2,0),B(2,0,0),C(0,1,0),D(-1,0,0),P(0,0,2),∴OE=(1,-1,0),OF=(0,-1,1),设平面OEF的法向量为m=(x,y,z),则解得m=(1,1,1).平面OAE的法向量为n=(0,0,1),∴cos〈m,n〉===.故二面角F-OE-A的余弦值为.2.如图,直三棱柱ABC-A1B1C1中,△ABC是等边三角形,D是BC的中点.(1)求证:A1B∥平面ADC1;(2)若AB=BB1=2,求A1D与平面AC1D所成角的正弦值.(1)证明因为三棱柱ABC-A1B1C1是直三棱柱,所以四边形A1ACC1是矩形.连接A1C交AC1于O,则O是A1C的中点,又D是BC的中点,所以在△ADC1中,OD∥A1B,因为A1B⊄平面ADC1,OD⊂平面ADC1,所以A1B∥平面ADC1.(2)解因为△ABC是等边三角形,D是BC的中点,所以AD⊥BC.以D为原点,建立如图所示空间坐标系D-xyz.由已知AB=BB1=2,得D(0,0,0),A(,0,0),A1(,0,2),C1(0,-1,2).则DA=(,0,0),DC1=(0,-1,2),设平面AC1D的法向量为n=(x,y,z),由得取z=1,则x=0,y=2,∴n=(0,2,1),又DA1=(,0,2),∴cos〈DA1,n〉==,设A1D与平面ADC1所成角为θ,则sinθ=|cos〈DA1,n〉|=,故A1D与平面ADC1所成角的正弦值为.3.如图,四边形ABCD为矩形,PD⊥平面ABCD,PD∥QA,QA=AD=PD.(1)求证:平面PQC⊥平面DCQ;(2)若二面角Q-BP-C的余弦值为-,求的值.(1)证明设AD=1,则DQ=,DP=2,又 PD∥QA,∴∠PDQ=∠AQD=45°,在△DPQ中,由余弦定理可得PQ=.∴DQ2+PQ2=DP2,∴PQ⊥DQ,又 PD⊥平面ABCD,∴PD⊥DC, CD⊥DA,DA∩PD=D,∴CD⊥平面ADPQ. PQ⊂平面ADPQ,∴CD⊥PQ,又 CD∩DQ=D,∴PQ⊥平面DCQ.又PQ⊂平面PQC,所以平面PQC⊥平面DCQ.(2)解如图,以D为坐标原点,DA,DP,DC所在直线为x轴,y轴,z轴,建立空间直角坐标系D-xyz.设AD=1,AB=m(m>0).依题意有D(0,0,0),C(0,0,m),P(0,2,0),Q(1,1,0),B(1,0,m),则CB=(1,0,0),BP=(-1,2,-m),PQ=(1,-1,0),设n1=(x1,y1,z1)是平面PBC的法向量,则即因此可取n1=(0,m,2).设n2=(x2,y2,z2)是平面PBQ的法向量,则即可取n2=(m,m,1).又 二面角Q-BP-C的余弦值为-,∴|cos〈n1,n2〉|=|-|.∴=整理得m4+7m2-8=0.又 m>0,解得m=1.因此,所求的值为1.[通关演练B组](建议用时:45分钟)1.在正三棱柱ABC-A1B1C1中,AB=2,AA1=,点D为AC的中点,点E在线段AA1上.(1)当AE∶EA1=1∶2时,求证DE⊥BC1;(2)是否存在点E,使二面角D-BE-A等于60°,若存在求AE的长;若不存在,请说明理由.(1)证明连接DC1,因为ABC-A1B1C1为正三棱柱,所以△ABC为正三角形,又因为D为AC的中点,所以BD⊥AC,又平面ABC⊥平面ACC1A1,所以BD⊥平面ACC1A1,所以BD⊥DE.因为AE∶EA1=1∶2,AB=2,AA1=,所以AE=,AD=1,所以在Rt△ADE中,∠ADE=30°,在Rt△DCC1中,∠C1DC=60°,所以∠EDC1=90°,即ED⊥DC1,又BD∩DC1=D,所以ED⊥平面BDC1,BC1⊂面BDC1,所以ED⊥BC1.(2)解假设存在点E满足条件,设AE=h.取A1C1的中点D1,连接DD1,则DD1⊥平面ABC,所以DD1⊥AD,DD1⊥BD,分别以DA,DB,DD1所在直线为x,y,z轴建立空间直角坐标系D-xyz,则A(1,0,0),B(0,,0),E(1,0,h),所以DB=(0,,0),DE=(1,0,h),AB=(-1,,0),AE=(0,0,h),设平面DBE的一个法向量为n1=(x1,y1,z1),则令z1=1,得n1=(-h,0,1),同理,平面ABE的一个法向量为n2=(x2,y2,z2),则∴n2=(,1,0).∴cos〈n1,n2〉==cos60°=.解得h=<,故存在点E,当AE=时,二面角D-BE-A等于60°.2.如图,在四棱锥P-ABCD中,平面PAC⊥平面ABCD,且PA⊥AC,PA=AD=2.四边形ABCD满...