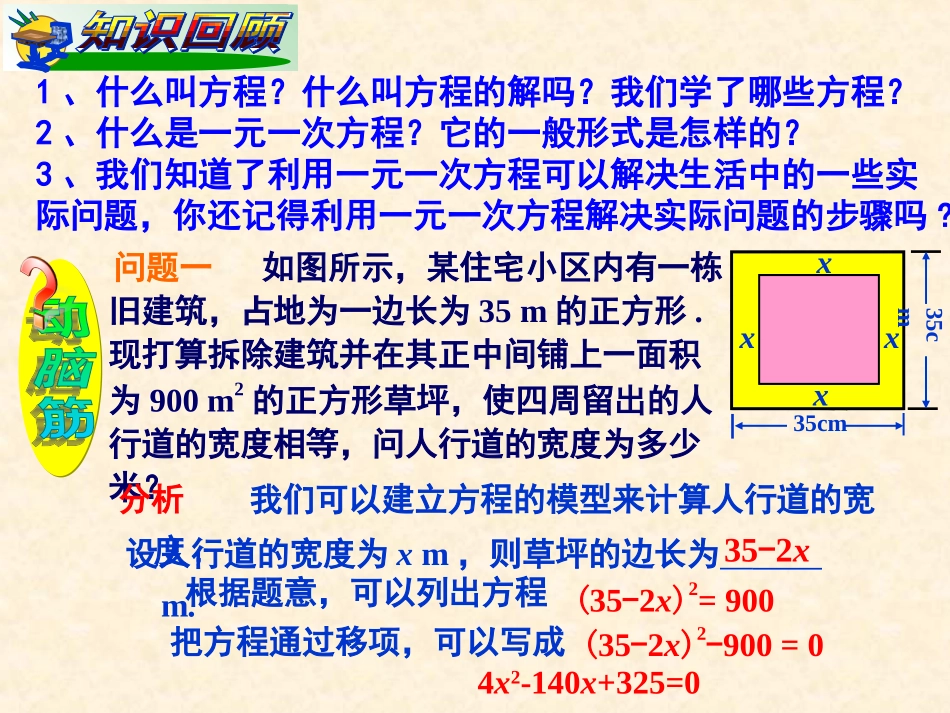
湘教版SHUXUE九年级上本节内容2.1ax2+bx+c=0x=-b±√b2-4ac2a1、什么叫方程?什么叫方程的解吗?我们学了哪些方程?2、什么是一元一次方程?它的一般形式是怎样的?3、我们知道了利用一元一次方程可以解决生活中的一些实际问题,你还记得利用一元一次方程解决实际问题的步骤吗?问题一如图所示,某住宅小区内有一栋旧建筑,占地为一边长为35m的正方形.现打算拆除建筑并在其正中间铺上一面积为900m2的正方形草坪,使四周留出的人行道的宽度相等,问人行道的宽度为多少米?35cm35cmxxxx分析我们可以建立方程的模型来计算人行道的宽度,设人行道的宽度为xm,则草坪的边长为m.35-2x根据题意,可以列出方程(35-2x)2=900把方程通过移项,可以写成(35-2x)2-900=04x2-140x+325=0问题二:据某市交通部门统计,2012年全市汽车拥有量市75万辆,两年后的2014年增加到108万辆,求该市两年来汽车拥有量的平均增长率?分析:设平均每年增长率为x.用代数式表示:2013年有汽车万辆。2014年有汽车万辆。75(1+x)75(1+x)2由此列出方程:.方程化简为:25x2+50x-11=075(1+x)2=108观察上述方程,它们有什么共同点?(1)它们分别含有几个未知数?(2)它们的左边分别是x和t的几次多项式?25x2+50x-11=00.01t2-2t=0.4x2-140x+325=0一个二次多项式结论从上述方程中受到启发,如果一个方程通过整理可以使右边为0,而左边是只含有一个未知数的二次多项式,那么这样的方程叫作一元二次方程.25x2+50x-11=04x2-140x+325=0ax2+bx+c=0(a,b,c是已知数,a≠0)ax2+bx+c=0(a,b,c是已知数,a≠0)其中a,b,c分别叫作二次项系数、一次项系数、常数项.一个一元二次方程可化成它的一般形式是:4x2-140x+325=0二次项系数是4、一次项系数是-140、常数项是325.0.01t2-2t=0.a=0.01,b=-2,c=025x2+50x-11=0a=25,b=50,c=-11要确定一元二次方程的二次项系数、一次项系数、常数项先将方程化成一般形式。举例下列方程是否为一元二次方程,若是,指出其二次项系数、一次项系数和常数项。(1)3x(1-x)+10=2(x+2)解:去括号,得:。整理,得:。3x-3x2+10=2x+4-3x2+x+6=0可以写成:3x2-x-6=0可以写成:3x2-x-6=0二次项系数是-3,一次项系数是1,常数项是6。(2)5x(x+1)-7=5x2+4解:去括号,得:。整理,得:。5x2+5x-7=5x2+45x-11=0这是一元一次方程,,不是一元二次方程。(3)(5-x)(x+1)+3=3(x-1)解:去括号,得:。5x+5-x2-x+3=3x-3整理,得:。x2-x-11=0二次项系数是1,一次项系数是-1,常数项是11。练习√1、判断下列方程是否为一元二次方程:①10x2=9()2(x-1)=3x()②③2x2-3x-1=0()()④⑤2xy-7=0()9x⑥2=5-4x()⑦4x2=5x()3y⑧2+4=5y()x21x2=0√√√√×××2、把一元二次方程(x-√5)(x+√5)+(2x-1)2=0化为一般形式,正确的是()A.5x2-4x-4=0B.x2-5=0C.5x2-2x+1=0D.5x2-4x+6=0A3、一元二次方程3x2+x-2=0的二次项系数和常数项分别为().A.3,1B.-1,-2C.3,-2D.-1,2C4、将方程3x2=5x+2化为一元二次方程的一般形式是:.3x2-5x-2=06、一块长和宽分别为40cm,28cm的矩形铁皮,在它的四角截去四个全等的小正方形,折成一个无盖的长方体盒子,使它的底面积为364cm2.截去的小正方形的边长应当是多少?5、一件衣服由300元经过两次降价后售价为243元,设这两次平均降价率为x,则所得方程是:。7、已知关于x的一元二次方程x2+ax+a=0的一个根是3,求a的值。8、方程(2a-4)x2-2bx+a=0,在什么条件下此方程为一元二次方程?在什么条件下此方程为一元一次方程?a≠2a=2,b≠09、已知关于x的一元二次方程(m-1)x2+3x-5m+4=0有一根为2,求m。10、P29B7300(1-x)2=2431、这节课你学到了什么知识?发现什么?2、一元二次方程的意义、一般形式是什么?3、在ax2+bx+c=0中,对a、b、c的值有什么条件限制?认识了一元二次方程,懂得数学知识来源于生活。由只含有一个未知数的二次多项式组成的整式方程叫作一元二次方程.一般形式是:ax2+bx+c=0(a,b,c是已知数,a≠0)ax2+bx+c=0(a,b,c是已知数,a≠0)其中a,b,c分别叫作二次项系数、一次项系数、常数项.作业:P28-----P29a≠0,b、c可以为0.