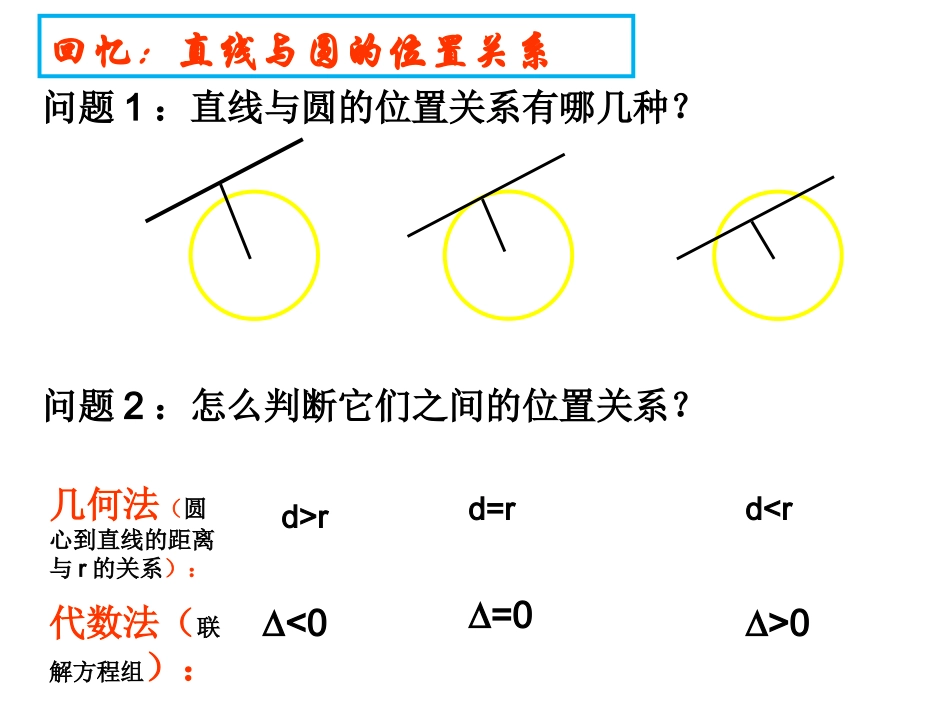
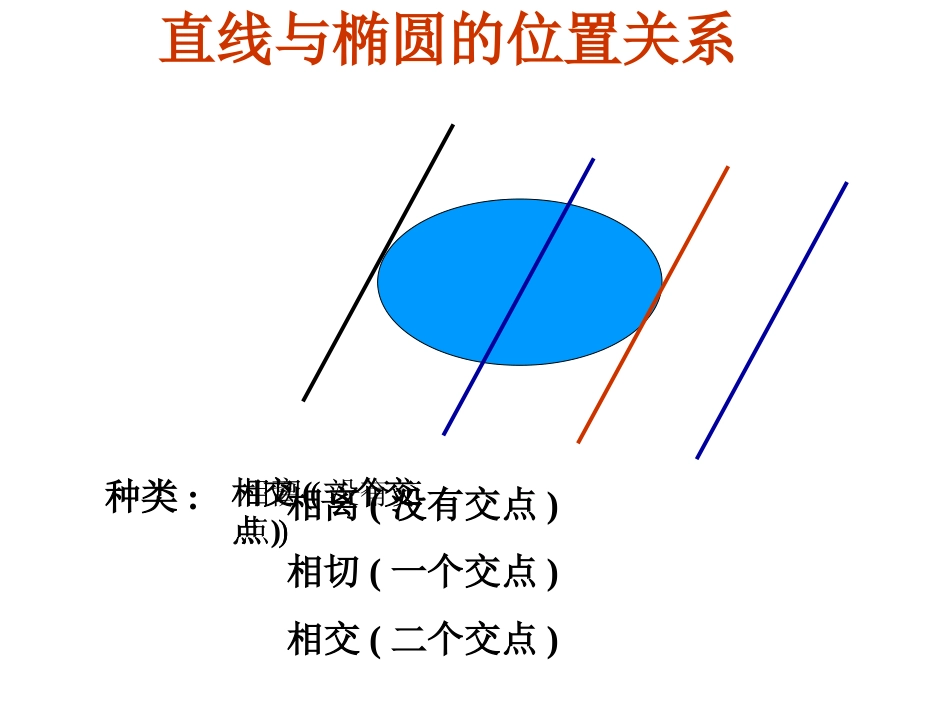
直线与椭圆的位置关系(1)问题2:怎么判断它们之间的位置关系?问题1:直线与圆的位置关系有哪几种?d>rd0∆<0∆=0几何法(圆心到直线的距离与r的关系):代数法(联解方程组):回忆:直线与圆的位置关系直线与椭圆的位置关系种类:相离(没有交点)相切(一个交点)相交(二个交点)相离(没有交点)相切(一个交点)相交(二个交点)1.位置关系:相交、相切、相离2代数法:联立直线与椭圆的方程消元得到二元一次方程组(1)>0△直线与椭圆相交有两个公共点;(2)=0△直线与椭圆相切有且只有一个公共点;(3)<0△直线与椭圆相离无公共点.通法知识点1.直线与椭圆的位置关系例1:已知直线y=x-与椭圆x2+4y2=2,判断它们的位置关系。21解:联立方程组21xyx2+4y2=2消去y01452xx因为∆>0-----(1)所以,方程(1)有两个根,则原方程组有两组解。题型一:直线与椭圆的位置关系上题中求线段AB的长?若能求到A,B两点的坐标呢?知识点2:弦长公式设直线AB的方程为:y=kx+b与椭圆交P1(x1,y1),P2(x2,y2)两点,求线段P1P2的长•若K不存在呢?2212121214PPkxxxx1212PPyy例2:已知点12FF、分别是椭圆22121xy的左、右焦点,过2F作倾斜角为4的直线交椭圆于A、B两点,求1FAB△的面积.分析:先画图熟悉题意,点1F到直线AB的距离易知,要求1FABS△,关键是求弦长AB.设1122(,),(,)AxyBxy.由直线方程和椭圆方程联立方程组例2:已知点12FF、分别是椭圆22121xy的左、右焦点,过2F作倾斜角为4的直线交椭圆于A、B两点,求1FAB△的面积.解:∵椭圆2212xy的两个焦点坐标12(1,0),(1,0)FF∴直线AB的方程为1yx设1122(,),(,)AxyBxy由22112yxxy消去y并化简整理得2340xx∴12124,03xxxx∴22221212121212()()2()2()4ABxxyyxxxxxx=423∵点1F到直线AB的距离d0(1)12=2∴112FABSdAB=142223=43.答:1FAB△的面积等于431、直线与椭圆的三种位置关系及判断方法;小结解方程组消去其中一元得一元二次型方程△<0相离△=0相切△>0相交2212121()4ABkxxxx2、弦长公式:练习:1、y=kx+1与椭圆恰有公共点,则m的范围()A、(0,1)B、(0,5)C、[1,5)∪(5,+∞)D、(1,+∞)2、过椭圆x2+2y2=4的左焦点作倾斜角为300的直线,则弦长|AB|=_______,C1522myx165谢谢!