双曲线及其标准方程(修改版)VIP免费

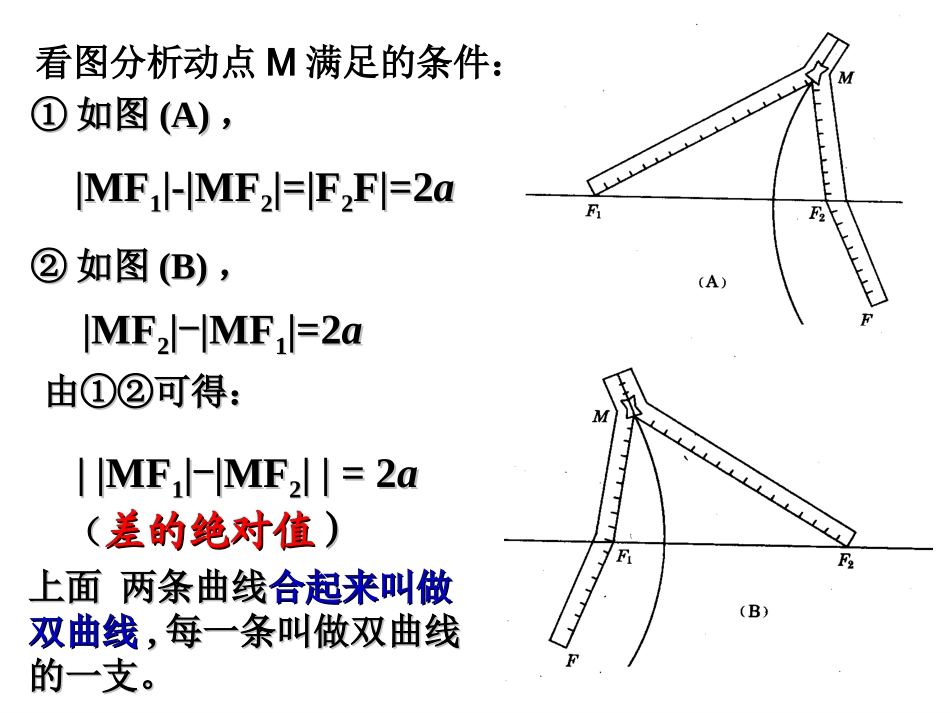
2.3.1双曲线及其标准方程2015年１2月椭圆的定义？1F2F0,c0,cXYOyxM,探索研究平面内与两个定点F1、F2的距离的和等于常数（大于｜F1F2｜）的点轨迹叫做椭圆。思考：如果把椭圆定义中的“距离之和”改为“距离之差”，那么点的轨迹是怎样的曲线？即“平面内与两个定点F1、F2的距离的差等于常数的点的轨迹”是什么？电脑演示①①如图如图(A)(A)，，|MF|MF11|-|MF|-|MF22|=|F|=|F22F|=2F|=2aa②②如图如图(B)(B)，，|MF|MF22||--|MF|MF11|=2|=2aa由①②可得：由①②可得：||MF||MF11||--|MF|MF22||=2||=2aa（（差的绝对值差的绝对值））上面两条曲线上面两条曲线合起来叫做合起来叫做双曲线双曲线,,每一条叫做双曲线每一条叫做双曲线的一支。的一支。看图分析动点M满足的条件：双曲线的定义平面内与两定点F1，F2的距离的差的绝对值等于常数（小于|F1F2|)的点的轨迹叫做双曲线.F1,F2-----焦点|F1F2|-----焦距记为2c||MF1|-|MF2||=2aF2F1M(这里c>a)设M（x,y）,双曲线的焦距为2c（c>0）,F1(-c,0),F2(c,0)常数为2aM以F1,F2所在的直线为X轴，线段F1F2的中点o为原点建立直角坐标系1.建系.2.设点．3.列式．||MF1|-|MF2||=2a如何求这优美的曲线的方程？4.化简.F1F2xOy.2)()(2222aycxycx即xyF2F1M焦点在y轴上的双曲线的标准方程是什么？•想一想.2|)()(|2222axcyxcy化简为：F1(0,-c),F2(0,c)222bac•例1、已知双曲线的焦点为F1(-5,0),F2(5,0)双曲线上一点到焦点的距离差的绝对值等于6，则(1)a=_______,c=_______,b=_______(2)双曲线的标准方程为______________(3)双曲线上一点Ｐ，若|PF1|=10,则|PF2|=_________3544或16||PF1|-|PF2||=6例2已知双曲线的焦点在x轴上，并且双曲线上的两点P1、P2的坐标分别（），（），求双曲线的标准方程。设法一：设法二：设法三：3,22,315变式已知双曲线上的两点P1、P2的坐标分别为（），（），求双曲线的标准方程。3,22,31511222mymx随堂练习变式变式::上述方程表示双曲线，则上述方程表示双曲线，则mm的取值范围是的取值范围是____________________________________m＜－2或m＞－1求适合下列条件的双曲线的标准方程①a=4,b=3，焦点在x轴上；②焦点为(0,－6),(0,6)，经过点(2,－5)已知方程表示焦点在y轴的双曲线，则实数m的取值范围是______________m＜－2191622yx1162022xy1、双曲线及其焦点，焦距的定义，双曲线的标准方程以及方程中的abc之间的关系课时小结：2、焦点位置的确定方法3、求双曲线标准方程关键（定位，定量）作业：P61习题2.3A.2B.2