《全等三角形（4）》课件VIP免费

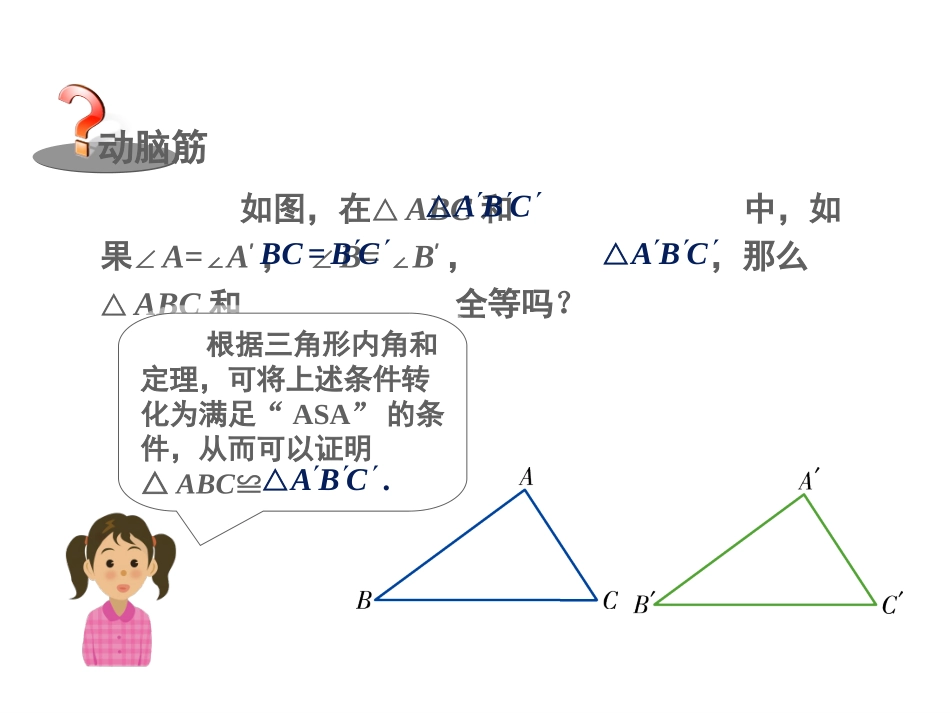
全等三角形全等三角形的判定（AAS）动脑筋如图，在△ABC和中，如果∠A=∠A′，∠B=∠B′，，那么△ABC和全等吗？△ABCBC=BC△ABC根据三角形内角和定理，可将上述条件转化为满足“ASA”的条件，从而可以证明△ABC≌根据三角形内角和定理，可将上述条件转化为满足“ASA”的条件，从而可以证明△ABC≌△ABC.在△ABC和中，ABC△∵∠A=∠A′，∠B=∠B′，∴∠C=∠C′.又∵，∠B=∠B′，BC=BC∴(ASA).ABCABC≌结论由此得到判定两个三角形全等的定理：两角分别相等且其中一组等角的对边相等的两个三角形全等.两角分别相等且其中一组等角的对边相等的两个三角形全等.通常可简写成“角角边”或“AAS”.例1已知：如图，∠B=∠D，∠1=2∠，求证：△ABC≌△ADC.举例证明∵∠1=2∠，∴∠ACB=∠ACD（同角的补角相等）.在△ABC和△ADC中，∴△ABC≌△ADC（AAS）.∠B=∠D，∠ACB=∠ACD，AC=AC，例2已知：如图，点B，F，C，E在同一条直线上，AC∥FD，∠A=∠D，BF=EC.求证：△ABC≌△DEF.举例证明∵AC∥FD，∴∠ACB=∠DFE.∵BF=EC，∴BF+FC=EC+FC，即BC=EF.在△ABC和△DEF中，∴△ABC≌△DEF（AAS）.∠A=∠D，∠ACB=∠DFE，BC=EF，练习1.已知：如图，∠1=2∠，AD=AE.求证：△ADC≌△AEB.∴△ADC≌△AEB（AAS）.∠1=2∠，∠A=∠A，AD=AE，证明∵在△ADC和△AEB中，2.已知：在△ABC中，∠ABC=∠ACB，BD⊥AC于点D，CE⊥AB于点E.求证：BD=CE.证明由题意可知△BEC和△BDC均为直角三角形，∵在Rt△BEC和Rt△CDB中，∴Rt△BECRt≌△CDB（AAS）.∠ABC=∠ACB，BC=BC，∠BEC=∠CDB=90°，