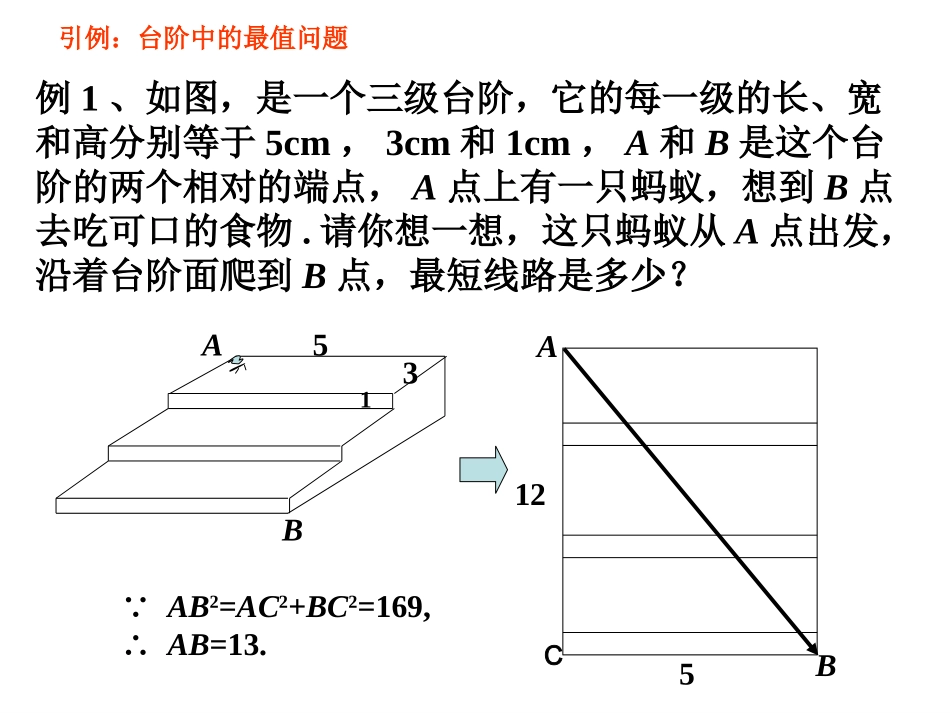
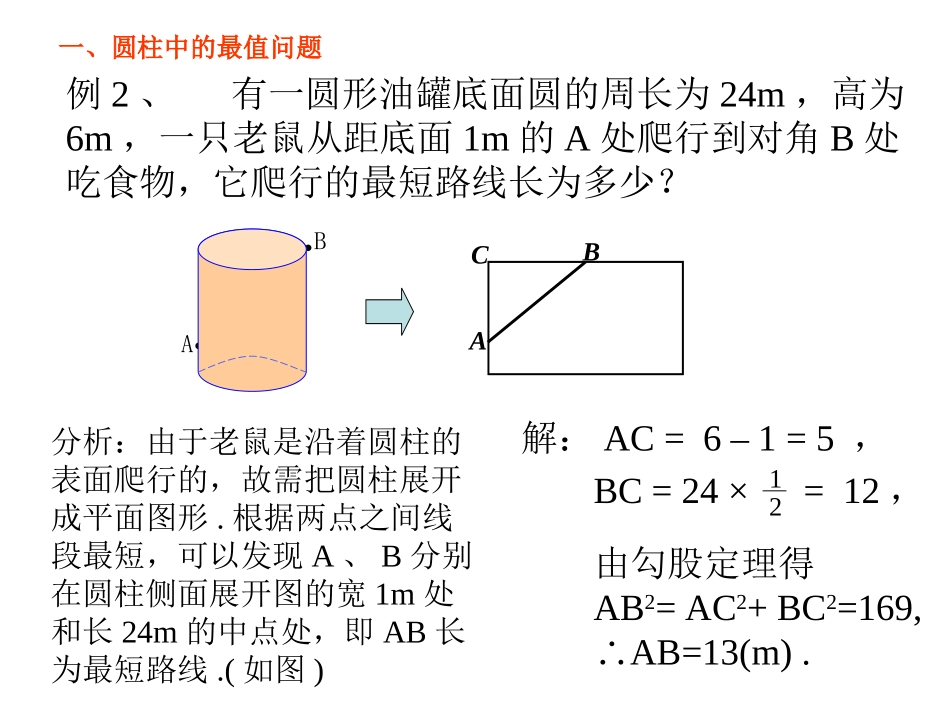
勾股定理的应用—求立体图形中的最短路径方亭慈济中学:杨启艳例1、如图,是一个三级台阶,它的每一级的长、宽和高分别等于5cm,3cm和1cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?BAAB531512引例:台阶中的最值问题∵AB2=AC2+BC2=169,∴AB=13.C一、圆柱中的最值问题例2、有一圆形油罐底面圆的周长为24m,高为6m,一只老鼠从距底面1m的A处爬行到对角B处吃食物,它爬行的最短路线长为多少?AB分析:由于老鼠是沿着圆柱的表面爬行的,故需把圆柱展开成平面图形.根据两点之间线段最短,可以发现A、B分别在圆柱侧面展开图的宽1m处和长24m的中点处,即AB长为最短路线.(如图)解:AC=6–1=5,BC=24×=12,由勾股定理得AB2=AC2+BC2=169,∴AB=13(m).21BAC小心解题哦有一圆形罐头底面圆的半径为6cm,高5cm,一只蚂蚁从距底面的A处爬行到对角B处吃食物,它爬行的最短路线长为多少?5cm6cmABABC二、正方体中的最值问题例3、如图,边长为1的正方体中,一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是().(A)3(B)√5(C)2(D)1AB分析:由于蚂蚁是沿正方体的外表面爬行的,故需把正方体展开成平面图形(如图).CABC21例4、如图,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点C1处(三条棱长如图所示),问怎样走路线最短?最短路线长为多少?ABA1B1DCD1C1214分析:根据题意分析蚂蚁爬行的路线有三种情况(如图①②③),由勾股定理可求得图1中AC1爬行的路线最短.ABA1B1D1C1①421AC1=√42+32=√25;②ABB1CA1C1412AC1=√62+12=√37;AB1D1DA1C1③412AC1=√52+22=√29.三、长方体中的最值问题怎样才能在最短的时间内,找到长方体表面上两点之间的最短路径?归纳提升:设长方体的长、宽、高分别为a、b、c,且a>b>c,则长方体表面上AB两点的最短路线为22()bca反思回顾,总结提高2+a2(b+c)、2+c2(a+b)2+b2(a+c)、提升:比较提升:比较的大小的大小即比较ab、bc、ac的大小。较短两段取和,最长段独一边41AB=●A●B135AB=10看谁算的快看谁算的快482●●AA●●BB小试牛刀(2008吉林)由若干个边长为1的小正方体摆放成的长方体,问在A处的蚂蚁要吃到B处的食物,最短要爬行多长?若食物在C处呢?●●AA●●BB●●CC●●AA●●CC225(42)61AB223(41)34AC●AB●C●●●BB●●AA要注意变式,灵活运用哦(2008吉林)(2008吉林)我能行如图,一个长方体形的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.(1)请你画出蚂蚁能够最快到达目的地的可能路径;(2)当AB=4,BC=4,CC1=5时,求蚂蚁爬过的最短路径的长;A备用图•如图,长方体的底面边长分别为1cm和3cm,高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要cm;如果从点A开始经过4个侧面缠绕n圈到达点B,那么所用细线最短需要cm.BA6cm3cm1cm巅峰对决1023664nA第1圈第2圈第n圈不下定决心培养思维习惯的人,便失去了生活中最大的乐趣——爱迪生多观察,多思考;多归纳,多总结小结:1、把几何体适当展开成平面图形2、利用“两点之间线段最短”的性质在平面图形上找出两点间的最短路径3、构造直角三角形,利用勾股定理找出最优解