两角差的余弦公式 (2)VIP免费

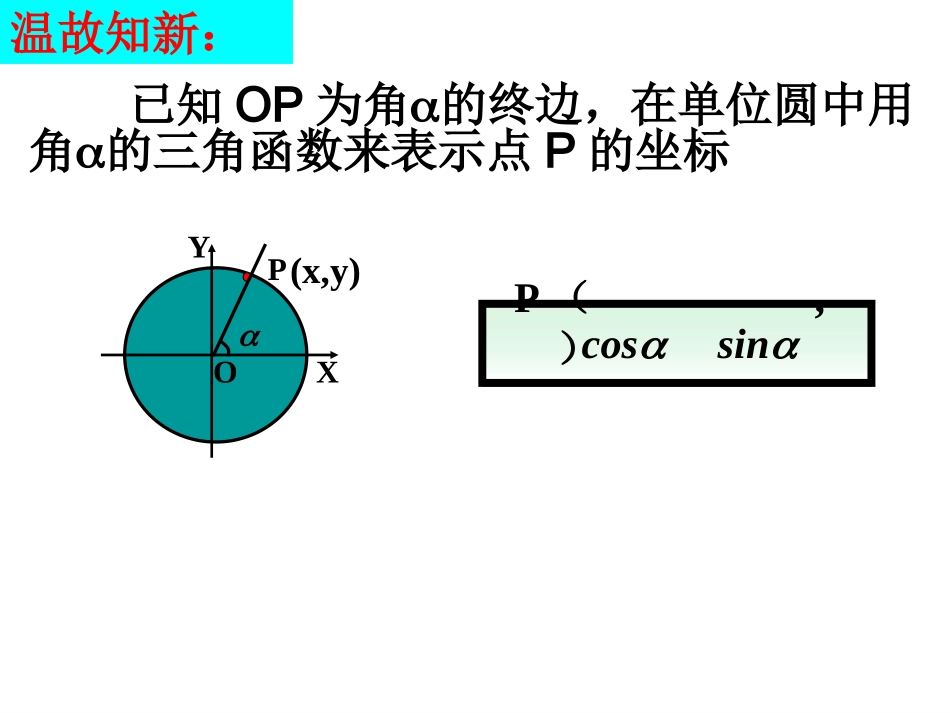
1、两角差的余弦公式是什么？2、两角差的余弦公式有哪些结构特征？(1)同名积(2)符号反简记作自主学习：)-cos(sinsincoscos()CCCSS，符号相反公式记忆“”已知OP为角的终边，在单位圆中用角的三角函数来表示点P的坐标P（,）POXY温故知新：(x,y)cossinBA-111-1yxo)sin,(cos)sin,(coscossincossin(2))cos(sinsincoscos(1)coscoscossinsin（）合作交流：请同学们思考、讨论以下问题：1、点A，点B的坐标及向量OA、OB的坐标是什么？2、向量OA、OB的数量积由坐标怎么表示？OA=（，）OB=（，）4、向量OA、OB的数量积由定义怎么表示？OA·OB=OA︱︱︱︱)cos(OBOA·OB===3、向量OA、OB的夹角是什么？例1.利用差角余弦公式求的值.cos15题后小结:1、把非特殊角拆分成特殊角的差.2、公式的直接应用.cos15cos4530解法1:30sin45sin30cos45coscos15cos6045解法2:45sin60sin45cos60cos2122232242622232221462.)cos(,135cos),,2(,54sin的值求是第三象限角，已知22512sin1cos11313,,24sin5解：因为2243cos1sin155由此得5cos,13又因为是第三象限角，所以题后小结:1、注意角的范围，也就是符号问题.2、公式的直接应用.想一想：去掉这个条件如何做？例2、例题讲解所以.6533)1312(54)135()53(sinsincoscos)cos(练习.已知2cos,3α=-α5求的值.cos4α解:2cos,3α=-α5∵∴24sin1cos5α=αcos()coscossinsin444-αα+α22422535210巩固练习：小结对于任意角α,β都有cos(α-β)=注意：1.公式的结构特点：2.公式的作用：求任意角α,β差的余弦值.(1)同名积(2)符号反两角差的余弦公式cosαcosβ+sinαsinβ