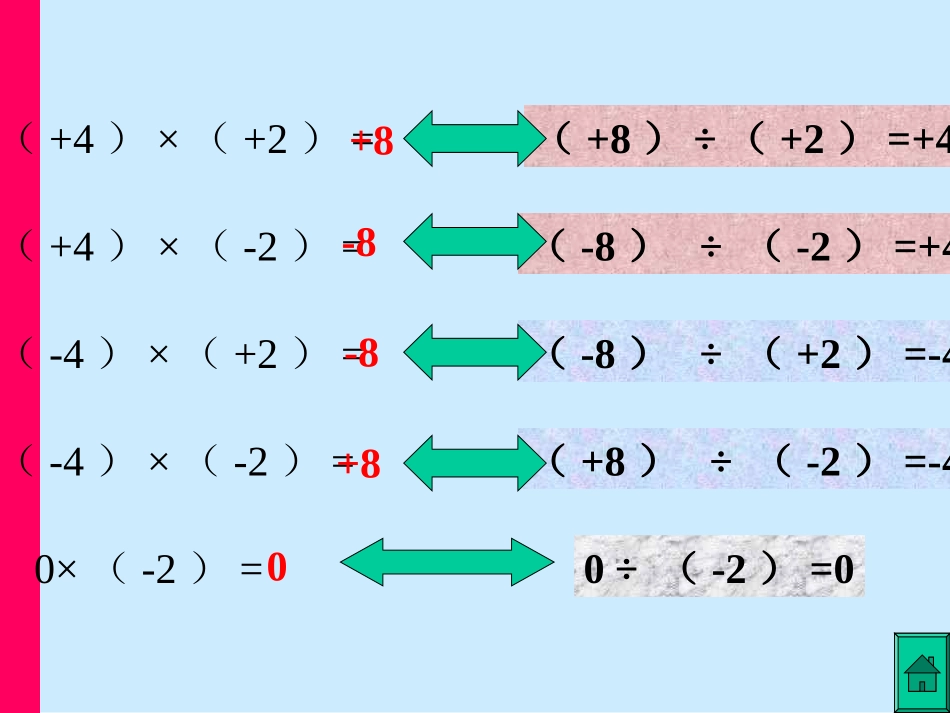
计算：）（）（218）（）（218）（）（218）（）（218）（210+4+4-4-40（+4）×（+2）=（+4）×（-2）=（-4）×（+2）=（-4）×（-2）=0×（-2）=+8-8-8+80（+8）÷（+2）=+4（-8）÷（-2）=+4（-8）÷（+2）=-4（+8）÷（-2）=-40÷（-2）=0（+8）÷（+2）=+4（-8）÷（-2）=+4（-8）÷（+2）=-4（+8）÷（-2）=-40÷（-2）=0）（）（218）（）（218）（）（218）（）（218）（210+4+4-4-40（+8）÷（+2）=（-8）÷（-2）=（-8）÷（+2）=（+8）÷（-2）=0÷（-2）=）（）（218）（）（218）（）（218）（）（218）（210+4+4-4-40有理数除法法则:除以一个不等于0的数,等于乘这个数的倒数.baba1)0(b（+8）÷（+2）=（-8）÷（-2）=（-8）÷（+2）=（+8）÷（-2）=0÷（-2）=）（）（218）（）（218）（）（218）（）（218）（210+4+4-4-40有理数的除法法则：两数相除，同号得正，异号得负，并把绝对值相除；零除以任何一个不等于零的数都是零。到现在为止我们有了两个除法法则，那么两个法则是不是都可以用于解决两数相除呢？两个法则分别更适合于什么样的两数相除呢？两个法则都可以用来求两个有理数相除.如果两数相除，能够整除的就选择法则二，不能够整除如果两数相除，能够整除的就选择法则二，不能够整除的就选择用法则一。的就选择用法则一。）（）（）（））（（）（））（（）（））（（计算下列各式：例21.83044363197621241.1）（））（（）（））（（）（））（（计算下列各式：例61172432116322232651.2)68(0).5()41()8).(4()3()15).(3()61()12).(2(9)36).(1(小结:一.有理数除法法则:1.)0(1bbaba2.两数相除，同号得正，异号得负，并把绝对值相除。0除以任何一个不等于0的数，都得0书本P384，6，