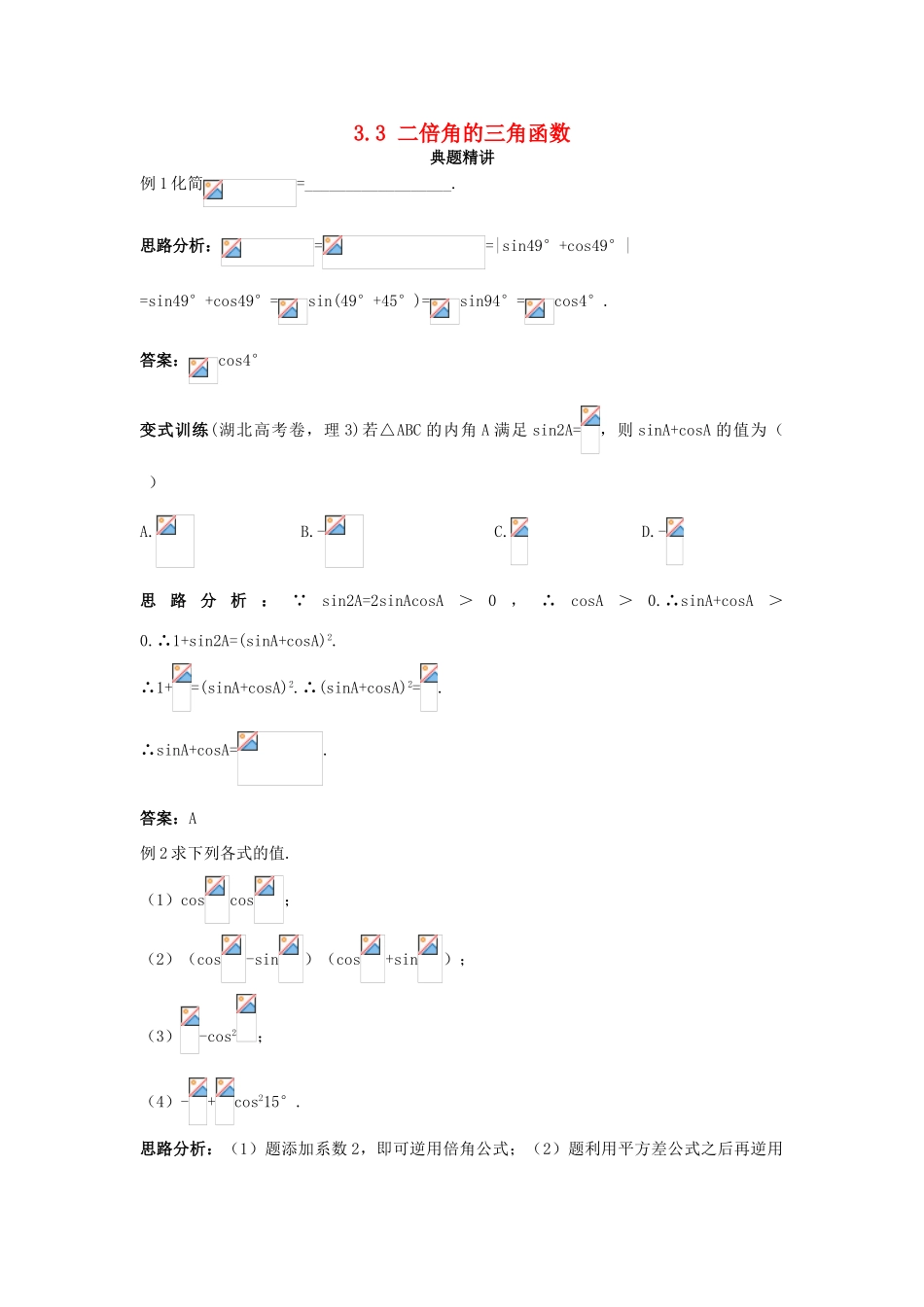
3.3二倍角的三角函数典题精讲例1化简=__________________.思路分析:==|sin49°+cos49°|=sin49°+cos49°=sin(49°+45°)=sin94°=cos4°.答案:cos4°变式训练(湖北高考卷,理3)若△ABC的内角A满足sin2A=,则sinA+cosA的值为()A.B.-C.D.-思路分析: sin2A=2sinAcosA>0,∴cosA>0.∴sinA+cosA>0.∴1+sin2A=(sinA+cosA)2.∴1+=(sinA+cosA)2.∴(sinA+cosA)2=.∴sinA+cosA=.答案:A例2求下列各式的值.(1)coscos;(2)(cos-sin)(cos+sin);(3)-cos2;(4)-+cos215°.思路分析:(1)题添加系数2,即可逆用倍角公式;(2)题利用平方差公式之后再逆用倍角公式;(3)中提取系数2后产生倍角公式的形式;(4)则需提取系数.解:(1)coscos=cossin=×2cossin=sin=.(2)(cos-sin)(cos+sin)=cos2-sin2=cos=.(3)-cos2=-(2cos2-1)=-cos=-.(4)-+cos215°=(2cos215°-1)=cos30°=.绿色通道:根据式子本身的特征,经过适当变形,进而利用公式,同时制造出特殊角,获得式子的值,在变形中一定要整体考虑式子的特征.变式训练求sin10°sin30°sin50°sin70°的值.思路分析:由sin30°=,原式可化为sin10°sin50°sin70°,再转化为cos20°cos40°cos80°,产生成倍数的角,增加一项sin20°,即可依次逆用倍角公式;也可使用三角中的对偶式,设而不求,达到变形的目的.解法一:sin10°sin30°sin50°sin70°=cos20°cos40°cos80°====.解法二:令M=sin10°sin30°sin50°sin70°,N=cos10°cos30°cos50°cos70°,则MN=(sin10°cos10°)(sin30°cos30°)(sin50°cos50°)(sin70°cos70°)=sin20°sin60°sin100°sin140°=cos10°cos30°cos50°cos70°=N.∴M=,即sin10°sin30°sin50°sin70°=.例3(2005江苏高考卷,10)若sin(-α)=,则cos(+2α)的值为()A.B.-C.D.思路分析:观察发现+2α=2(+α),而(+α)+(-α)=,则cos(+α)=sin(-α),cos(+2α)=2cos2(+α)-1=2sin2(-α)-1=.答案:A绿色通道:通过角的形式的变化,生成所求的角或再变形即得所求角,是三角变换的重要方式,求解时应当对所给角有敏锐的感觉,这种感觉的养成要靠平时经验的积累.变式训练1已知sin(+α)sin(-α)=,且α∈(,π),求sin4α的值.思路分析:发现+α与-α是互余关系,将其中一个角的三角函数变为另一个的余名三角函数,即可产生倍角公式的形式,逆用倍角公式可得2α的三角函数值,进一步可求4α的正弦值.解: (+α)+(-α)=,∴sin(-α)=cos(+α). sin(+α)sin(-α)=,∴2sin(+α)cos(+α)=.∴sin(+2α)=.∴cos2α=.又 α∈(,π),∴2α∈(π,2π).∴sin2α=.∴sin4α=2sin2αcos2α=.变式训练2设5π<θ<6π,cos=a,则sin的值等于()A.B.C.D.思路分析:显然是的一半,可以直接应用公式. 5π<θ<6π,∴<<3π,<<.∴sin=.答案:D例4(2006全国高考卷Ⅱ,理2)函数y=sin2xcos2x的最小正周期是()A.2πB.4πC.D.思路分析:将函数的解析式化为y=Asin(ωx+φ)的形式.y=sin2xcos2x=sin4x,则T=.答案:D绿色通道:讨论三角函数的周期性时,先化简解析式再求周期.化简的手段是:利用和差、倍角、半角等三角公式;化简的结果是:将三角函数的解析式化为y=Asin(ωx+φ)的形式,再利用公式T=得周期.变式训练(2006陕西高考卷,理17)已知函数f(x)=sin(2x-)+sin2(x-)(x∈R).(1)求函数f(x)的最小正周期;(2)求使函数f(x)取得最大值的x集合.思路分析:将三角函数的解析式化为y=Asin(ωx+φ)+b的形式,再讨论周期和最值.解:(1)f(x)=sin(2x-)+1-cos(x-)=2[sin(x-)-cos(x-)]+1=2sin[2(x-)-]+1=2sin(2x-)+1,∴T==π.(2)当f(x)取最大值时,sin(2x-)=1,有2x-=2kπ+(k∈Z).∴x=kπ+.即使函数f(x)取得最大值的x集合为{x∈R|x=kπ+,k∈Z}.问题探究问题试用tan表示sinα,cosα,tanα.导思:看到α和,联想到α=2(),因此从二倍角公式的角度来探讨.探究:可以由倍角公式直接获得tanα=;正弦、余弦只要在倍角公式中添加分母,再分子、分母同除以cos2可得sinα=2sincos=,cosα=cos2-sin2=.用tan来表示sinα、cosα和tanα的关系式如下:sinα=tanα=.这三个公...