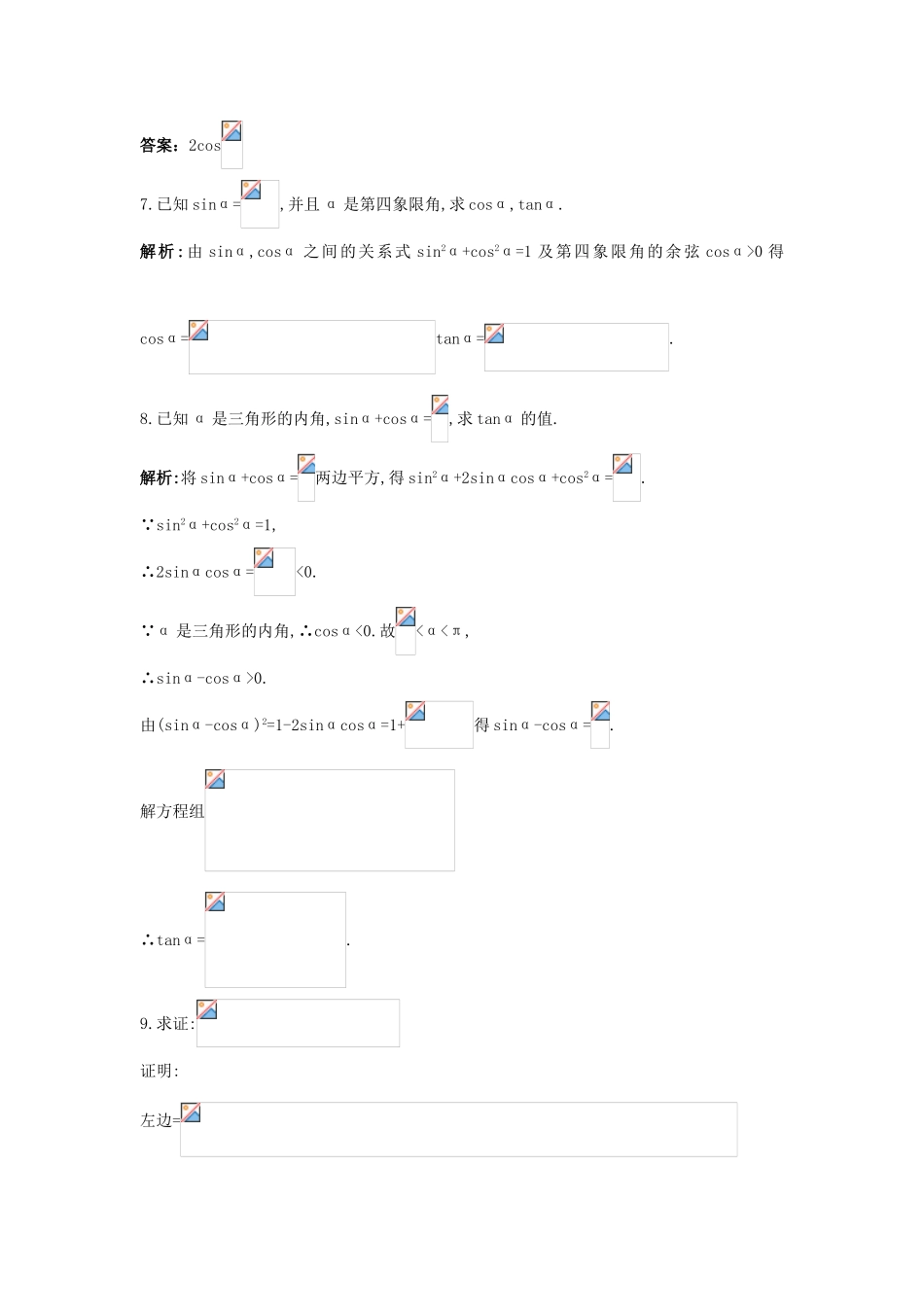
3.1同角三角函数的基本关系课后导练基础达标1.已知cosθ=,且θ为第二象限角,则tanθ等于()A.B.C.D.解析:∵θ为第二象限角,∴sinθ=,tanθ=.答案:B2.已知tanα=2,则的值是()A.1B.C.-1D.-解析:原式==1.答案:A3.已知sinαcosα=,且<α<,则cosα-sinα的值等于()A.B.C.D.±解析:(cosα-sinα)2=1-2sinαcosα=1-2×=,又<α<,cosα-sinα<0.∴cosα-sinα=.答案:C4.已知,则α的终边在()A.第一象限B.第二象限C.第一或第三象限D.第三或第四象限解析:,若这两部分相等,则sinα与cosα同号.∴α在第一或第三象限.答案:C5.若β∈[0,2π),且=sinβ-cosβ,则β的取值范围是()A.[0,)B.[,π]C.[π,]D.[,2π)解析:∵=|sinβ|+|cosβ|=sinβ-cosβ,∴sinβ≥0,cosβ≤0,∴β是第二象限角(包括x轴负半轴和y轴正半轴).∵0≤β<2π,∴β∈[,π].答案:B6.(0<α<)=_____________.解析:要灵活运用“1”,同时注意开方时符号的选取.原式==|sin-cos|+|sin+cos|.∵0<α<,∴0<<.∴sin-cos<0,sin+cos>0.∴上式=cos-sin+sin+cos=2cos.答案:2cos7.已知sinα=,并且α是第四象限角,求cosα,tanα.解析:由sinα,cosα之间的关系式sin2α+cos2α=1及第四象限角的余弦cosα>0得cosα=tanα=.8.已知α是三角形的内角,sinα+cosα=,求tanα的值.解析:将sinα+cosα=两边平方,得sin2α+2sinαcosα+cos2α=.∵sin2α+cos2α=1,∴2sinαcosα=<0.∵α是三角形的内角,∴cosα<0.故<α<π,∴sinα-cosα>0.由(sinα-cosα)2=1-2sinαcosα=1+得sinα-cosα=.解方程组∴tanα=.9.求证:证明:左边==右边.∴原式成立.10.已知tanα=2,求下列各式的值:(1);(2)解析:(1)=-1.或∵tanα==2,∴sinα=2cosα.∴原式==-1.(2).综合运用11.已知A为三角形内角,且sinAcosA=,则cosA-sinA的值为()A.B.±C.±D.解析:利用(sinθ±cosθ)2=1±2sinθcosθ求解.∵A为三角形内角,则A∈(0,π).又∵sinAcosA=<0,∴sinA>0,cosA<0.∴(sinA-cosA)2=1-2sinAcosA=1-2×()=.又∵cosA-sinA<0,∴cosA-sinA=.答案:D12.已知f(x)=,若α∈(,π),则f(cosα)+f(-cosα)可化简为_______________.解析:f(cosα)+f(-cosα)=答案:13.求证:=sinα+cosα.证明:==sinα+cosα14.已知sinαcosα>0,且sinαtanα>0.化简cos解析:由sinαcosα>0,知α为第一、三象限角.由sinαtanα>0,知α为第一、四象限角.∴α为一象限角,∴为第一、三象限角.当为第一象限角时,原式=cos·1=2.当为第三象限角时,原式=-2.15.是否存在角α、β,α∈(-,),β∈(0,π),使解析:将已知化为sinα=sinβ,①cosα=cosβ,②①2+②2,得sin2α+3(1-sin2α)=2,∴sin2α=,sinα=±.∵-<α<,∴α=或-.当α=时,由②得cosβ=.又β∈(0,π),∴β=.当α=-时,由②得cosβ=.又β∈(0,π),∴β=.∴存在使两个等式同时成立.拓展探究16.若f(x)=1-2a-2acosx-2sin2x的最小值为f(a).(1)用a表示f(a)的表达式;(2)求能使f(a)=的a值,并求当a取此值时f(x)的最大值.解析:(1)f(x)=1-2a-2acosx-2sin2x=1-2a-2acosx-2+2cos2x=2(cosx-)2-a2-2a-1.①当>1,即a>2且cosx=1时,f(x)取得最小值.即f(a)=1-4a;②当-1≤≤1,即-2≤a≤2且cosx=时,f(x)取得最小值,即f(a)=-a2-2a-1;③当<-1,即a<-2且cosx=-1时,f(x)取得最小值,即f(a)=1;综上得f(a)=(2)若f(a)=,则a只能在[-2,2]内,∴-a2-2a-1=,得a=-1,此时f(x)=2(cosx+)2+;当cosx=1时,f(x)有最大值5.