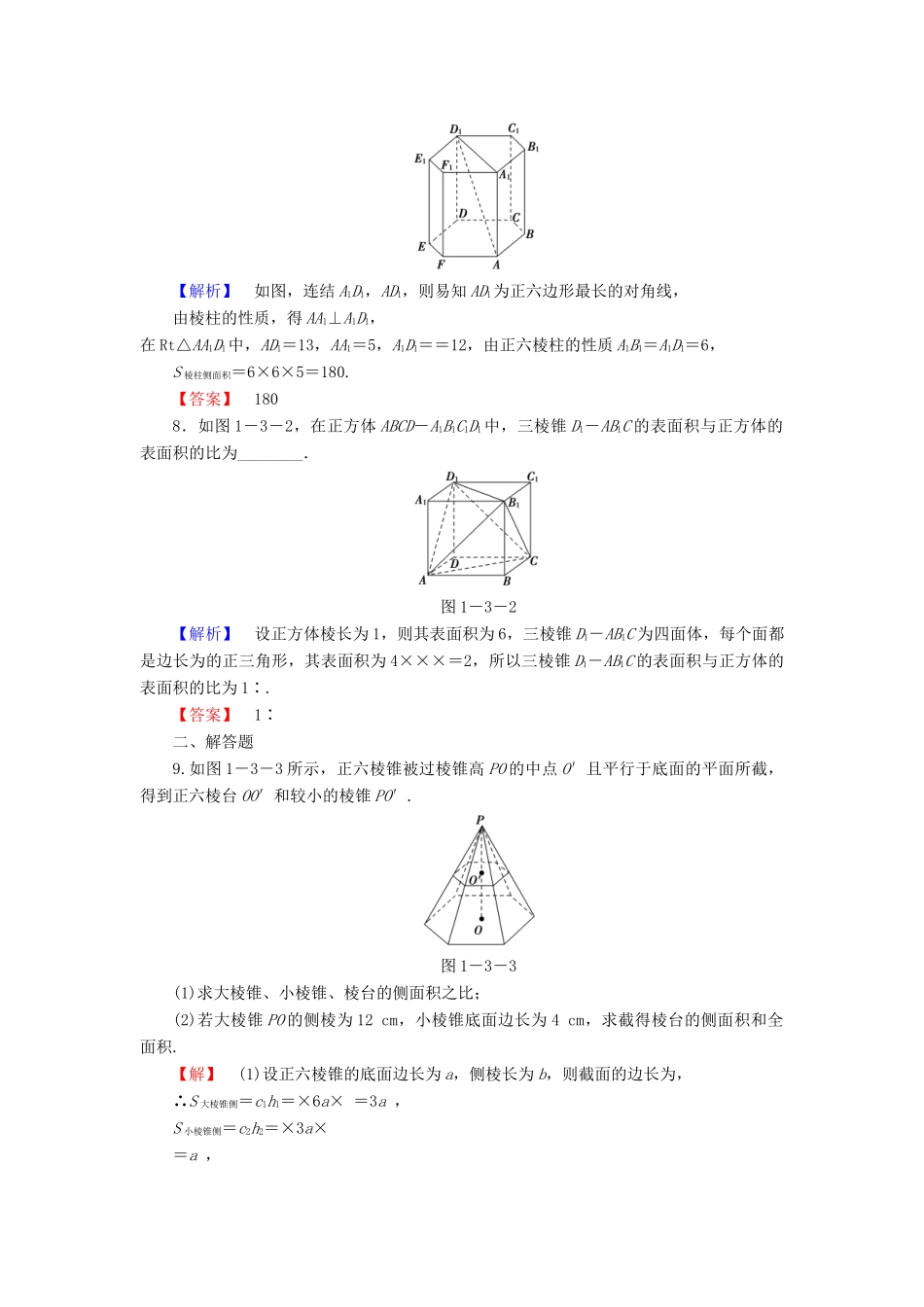
1.3.1空间几何体的表面积(建议用时:45分钟)[学业达标]一、填空题1.下列有四个结论,其中正确的是________.(1)各个侧面都是等腰三角形的棱锥是正棱锥;(2)三条侧棱都相等的棱锥是正棱锥;(3)底面是正三角形的棱锥是正三棱锥;(4)顶点在底面上的射影既是底面多边形的内心,又是外心的棱锥必是正棱锥.【解析】(1)不正确,正棱锥必备两点,一是底面为正多边形,二是顶点在底面内的射影是底面的中心;(2)缺少第一个条件;(3)缺少第二个条件;而(4)可推出以上两个条件,故正确.【答案】(4)2.一个正四棱柱的对角线的长是9cm,全面积等于144cm2,则这个棱柱的侧面积为________cm2.【解析】设底面边长,侧棱长分别为acm,lcm,∴∴S侧=4×4×7=112cm2.【答案】1123.斜三棱柱的底面是边长为5的正三角形,侧棱长为4,侧棱与底面两边所成角都是60°,那么这个斜三棱柱的侧面积是________.【解析】由题意可知S侧=2×5×4×sin60°+5×4=20+20.【答案】20+204.一个圆台的母线长等于上、下底面半径和的一半,且侧面积是32π,则母线长为________.【解析】 l=,∴S侧=π(R+r)l=2πl2=32π,∴l=4.【答案】45.已知正三棱台的上底面边长为2,下底面边长为4,高为,则正三棱台的侧面积S1与底面积之和S2的大小关系为__________.【解析】斜高h′==,S1=×(3×2+3×4)×=9,S2=×22+×42=5,∴S1>S2.【答案】S1>S26.圆锥侧面展开图的扇形周长为2m,则全面积的最大值为________.【解析】设圆锥底面半径为r,母线为l,则有2l+2πr=2m.∴S全=πr2+πrl=πr2+πr(m-πr)=(π-π2)r2+πmr.∴当r==时,S全有最大值.【答案】7.正六棱柱的高为5,最长的对角线为13,则它的侧面积为__________.【解析】如图,连结A1D1,AD1,则易知AD1为正六边形最长的对角线,由棱柱的性质,得AA1⊥A1D1,在Rt△AA1D1中,AD1=13,AA1=5,A1D1==12,由正六棱柱的性质A1B1=A1D1=6,S棱柱侧面积=6×6×5=180.【答案】1808.如图1-3-2,在正方体ABCD-A1B1C1D1中,三棱锥D1-AB1C的表面积与正方体的表面积的比为________.图1-3-2【解析】设正方体棱长为1,则其表面积为6,三棱锥D1-AB1C为四面体,每个面都是边长为的正三角形,其表面积为4×××=2,所以三棱锥D1-AB1C的表面积与正方体的表面积的比为1∶.【答案】1∶二、解答题9.如图1-3-3所示,正六棱锥被过棱锥高PO的中点O′且平行于底面的平面所截,得到正六棱台OO′和较小的棱锥PO′.图1-3-3(1)求大棱锥、小棱锥、棱台的侧面积之比;(2)若大棱锥PO的侧棱为12cm,小棱锥底面边长为4cm,求截得棱台的侧面积和全面积.【解】(1)设正六棱锥的底面边长为a,侧棱长为b,则截面的边长为,∴S大棱锥侧=c1h1=×6a×=3a,S小棱锥侧=c2h2=×3a×=a,S棱台侧=(c1+c2)(h1-h2)=(6a+3a)×=a,∴S大棱锥侧∶S小棱锥侧∶S棱台侧=4∶1∶3.(2)S侧=(c1+c2)(h1-h2)=144(cm2),S上=6××4×4×sin60°=24(cm2),S下=6××8×8×sin60°=96(cm2),∴S全=S侧+S上+S下=144+120(cm2).10.圆台的一个底面周长是另一个底面周长的3倍,轴截面的面积为392cm2,母线与轴的夹角为45°,求这个圆台的高、母线长和底面半径.【解】法一:圆台的轴截面如图所示,根据题意可设圆台的上、下底面半径分别为xcm和3xcm.即A′O′=xcm,AO=3xcm(O′,O分别为上、下底面圆心),过A′作AB的垂线,垂足为点D.在Rt△AA′D中,∠AA′D=45°,AD=AO-A′O′=2xcm,所以A′D=AD=2xcm,又S轴截面=(A′B′+AB)·A′D=×(2x+6x)×2x=392(cm2),所以x=7.综上,圆台的高OO′=14cm,母线长AA′=OO′=14cm,上、下底面的半径分别为7cm和21cm.法二:圆台的轴截面如图所示,根据题意可设圆台的上、下底面半径分别为xcm和3xcm,延长AA′,BB′交OO′的延长线于点S(O′,O分别为上、下底面圆心).在Rt△SOA中,∠ASO=45°,所以SO=AO=3xcm,又SO′=A′O′=xcm,所以OO′=2xcm.又S轴截面=×(2x+6x)×2x=392(cm2),所以x=7.综上,圆台的高OO′=14cm,母线长AA′=OO′=14cm,上、下底面的半径分别为7cm,21cm.[能力...