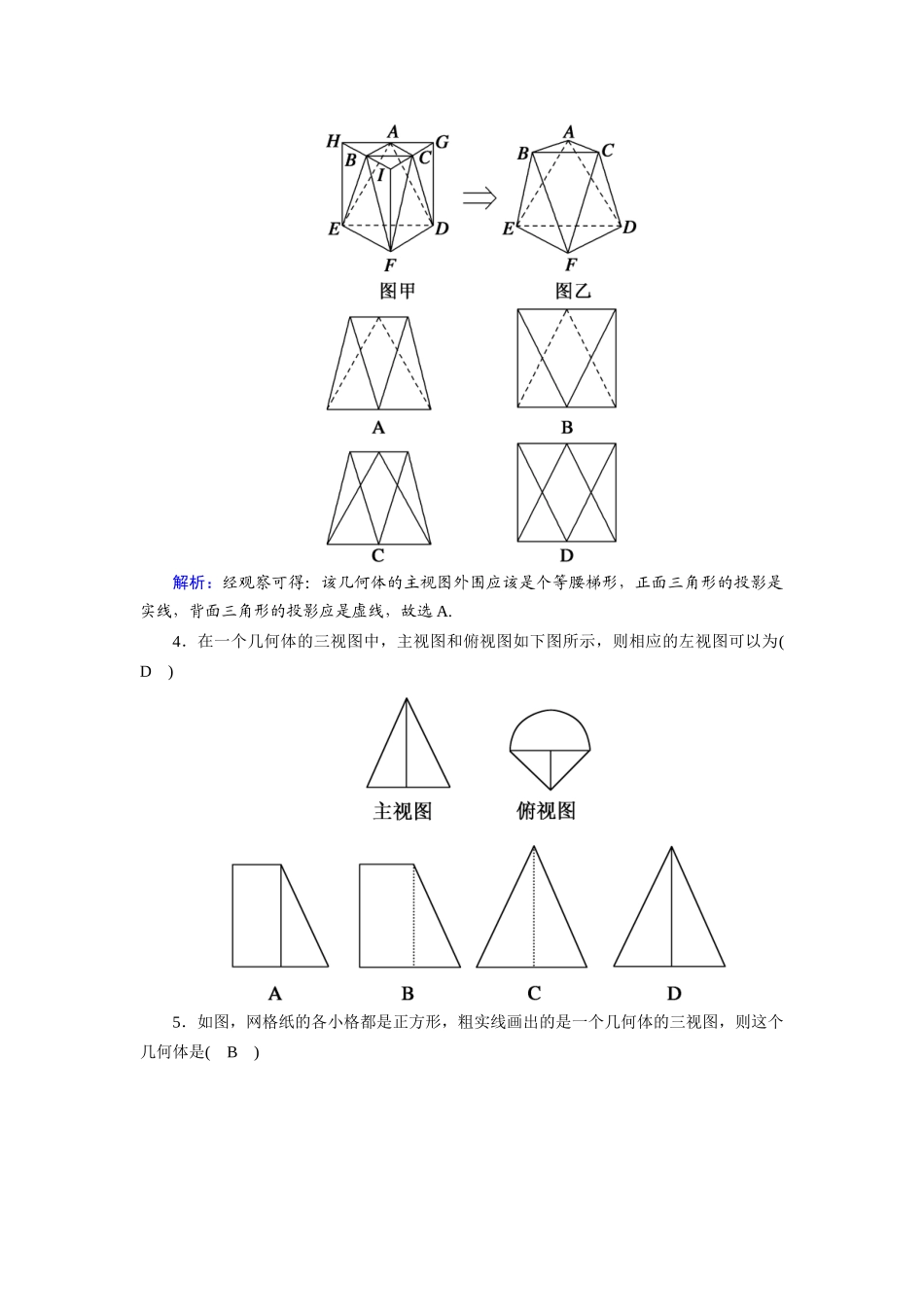
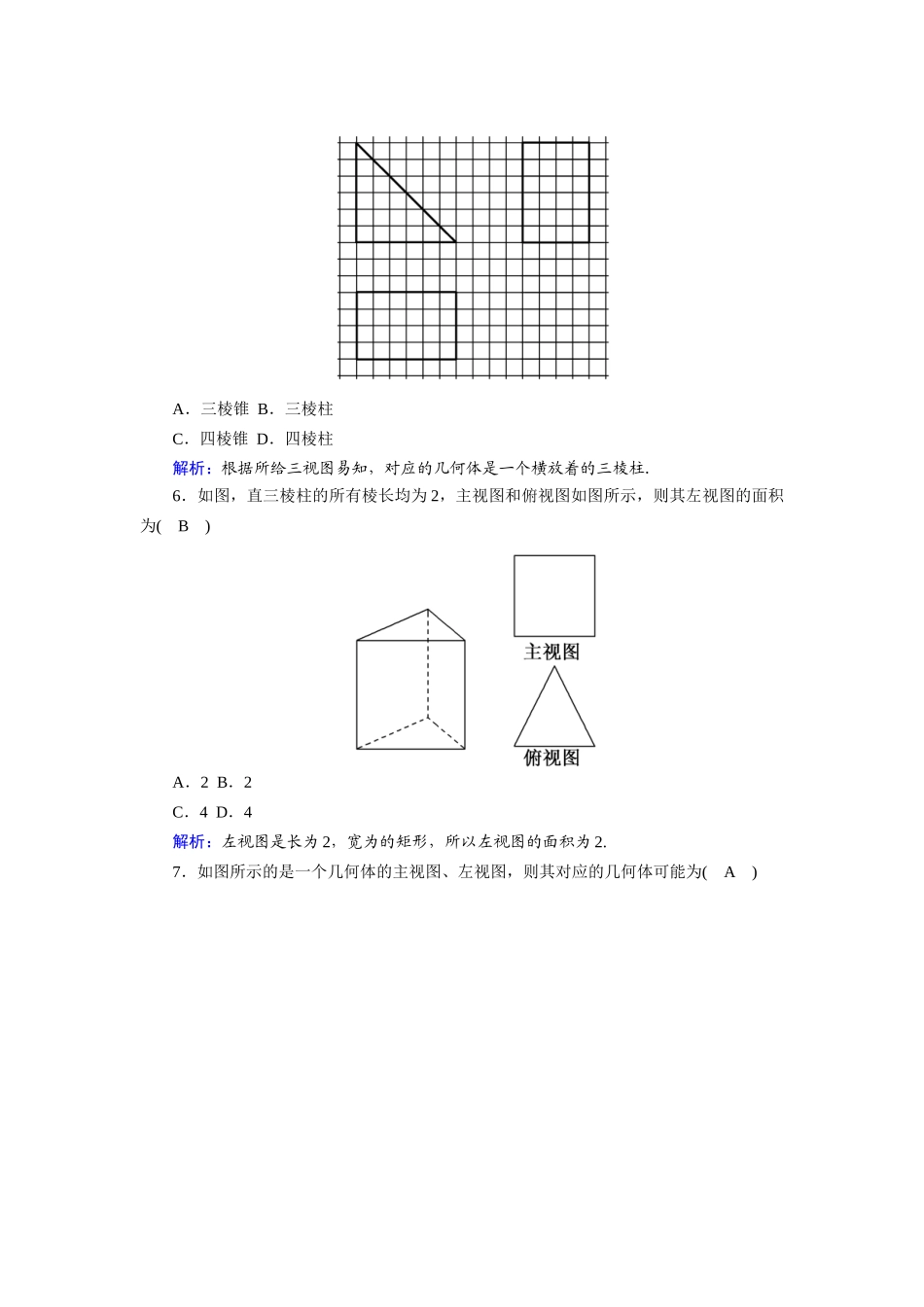
课时作业4三视图时间:45分钟——基础巩固类——一、选择题1.对几何体的三视图,下列说法正确的是(C)A.三视图反映几何体的长和宽B.俯视图反映几何体的长和高C.左视图反映几何体的高和宽D.主视图反映几何体的高和宽解析:在几何体的三视图中,主视图反映物体的长和高,左视图反映物体的宽和高,俯视图反映物体的长和宽,根据此规律可得结论.2.如图所示的图形中,是四棱锥的三视图的是(B)解析:A中,俯视图为圆,不正确;C中,主视图、左视图不是三角形,也不正确;D中,俯视图为三角形,显然不是四棱锥.故选B.3.将正三棱柱截去三个角(如图甲所示,A,B,C分别是三边的中点)得到几何体(如图乙),则该几何体的主视图为(A)解析:经观察可得:该几何体的主视图外围应该是个等腰梯形,正面三角形的投影是实线,背面三角形的投影应是虚线,故选A.4.在一个几何体的三视图中,主视图和俯视图如下图所示,则相应的左视图可以为(D)5.如图,网格纸的各小格都是正方形,粗实线画出的是一个几何体的三视图,则这个几何体是(B)A.三棱锥B.三棱柱C.四棱锥D.四棱柱解析:根据所给三视图易知,对应的几何体是一个横放着的三棱柱.6.如图,直三棱柱的所有棱长均为2,主视图和俯视图如图所示,则其左视图的面积为(B)A.2B.2C.4D.4解析:左视图是长为2,宽为的矩形,所以左视图的面积为2.7.如图所示的是一个几何体的主视图、左视图,则其对应的几何体可能为(A)解析:根据主视图和左视图中对角线的位置及实虚,可知只有选项A符合.8.某几何体的三视图(单位:cm)如图所示,则此几何体的表面积是(D)A.90cm2B.129cm2C.132cm2D.138cm2解析:由三视图可知,几何体如图所示:所以表面积是2×4×6+2×3×4+3×6+3×3+3×4+3×5+2××3×4=138(cm2).二、填空题9.如图所示是一个空间几何体的三视图,则该几何体为正六棱台.10.分别把下图所示六棱柱的三视图名称填在下面相应的横线上.11.图(1)是某组合体的主视图与左视图(其中AB=AC,四边形BCDE为矩形),则该组合体的俯视图可以是图(2)中的①②③④(把你认为正确的序号都填上).解析:由主视图与左视图相同可得,该几何体可以是由共底面的正四棱柱与正四棱锥组合而成,则其俯视图为图①;该几何体可以是由正四棱柱与底面直径等于正四棱柱底面边长的圆锥组合而成,则其俯视图为图④;该几何体可以是由共底面的圆柱与圆锥组合而成,则其俯视图为图③;该几何体可以是由圆柱与底面正方形边长等于圆柱底面直径的正四棱锥组合而成,则其俯视图为图②.综上可得,该组合体的俯视图可以是①②③④.三、解答题12.如图所示的是一个几何体的三视图,请你画出它的实物图,并说出它的主要结构特征.解:由几何体的三视图可知,此几何体是组合体,是从一个圆柱中挖去一个以圆柱的上底面为底面,下底面圆心为顶点的圆锥而得到的,它的实物图如图所示.13.若一个正三棱柱的三视图如图所示,求这个三棱柱的高和底面边长.解:高与左视图的高一致:h=2,∵底面三角形的高为2,在等边三角形中,可知其底面边长为4.∴h=2,底面边长为4.——能力提升类——14.如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为(C)A.2B.2C.4D.4解析:依据多面体的三视图,画出它的直观图,如图中的三棱锥E-FC1C,其中ABCD-A1B1C1D1是棱长为4的正方体,点E,F分别为棱BB1,DD1的中点,所以三棱锥E-FC1C中,最长的棱的长度为EF==4.15.已知正三棱锥V-ABC的主视图、俯视图如图所示,其中VA=4,AC=2,求该三棱锥的表面积.解:由主视图与俯视图可得正三棱锥的示意图(如图所示),且VA=VB=VC=4,AB=BC=AC=2.取BC的中点D,连接VD,则VD⊥BC,有VD===,则S△VBC=×VD×BC=××2=,S△ABC=×(2)2×=3.所以三棱锥V-ABC的表面积为3S△VBC+S△ABC=3+3=3(+).