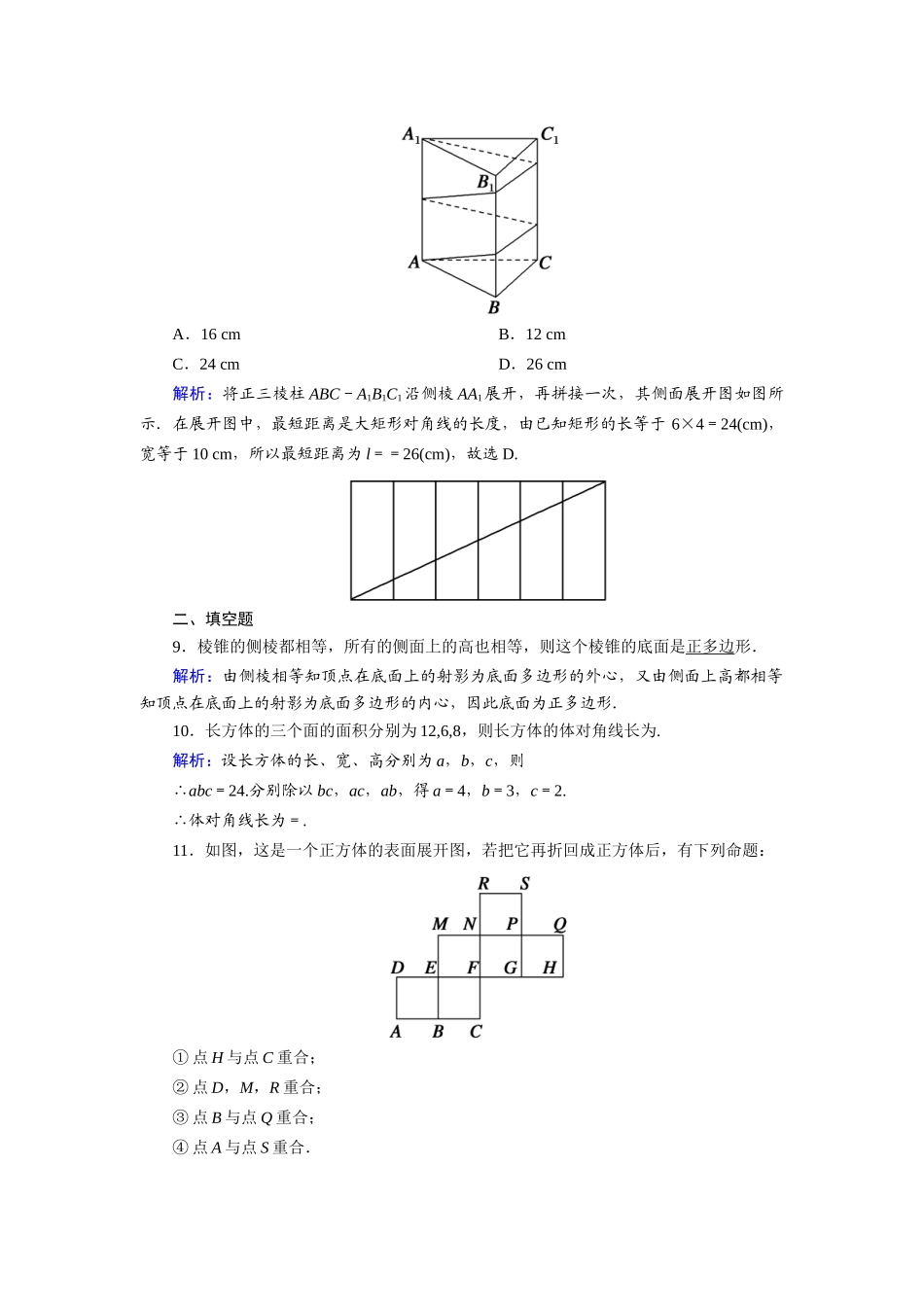
课时作业2简单多面体时间:45分钟——基础巩固类——一、选择题1.下列命题中正确的是(D)A.有两个面平行,其余各面都是四边形的几何体叫棱柱B.有两个面平行,其余各面都是梯形的几何体叫棱台C.有一个面是多边形,其余各面都是三角形的几何体叫棱锥D.棱台各侧棱的延长线交于一点解析:A选项中,缺少条件:其余各面都是四边形,且每相邻四边形的公共边平行;B选项中,缺少条件:每相邻梯形的公共边相交于一点;C选项中,缺少条件:其余各面三角形有公共顶点.2.如图所示,在三棱台A′B′C′-ABC中,截去三棱锥A′-ABC,则剩余部分是(B)A.三棱锥B.四棱锥C.三棱柱D.组合体解析:剩余部分是四棱锥A′-BB′C′C.3.一个棱锥的各条棱都相等,那么这个棱锥一定不是(D)A.三棱锥B.四棱锥C.五棱锥D.六棱锥解析:因为棱锥的各条棱都相等,所以侧面都是正三角形,又因为顶点处的各个面上顶角之和小于360°,从而侧面数小于6,故选D.4.下列说法错误的是(D)A.多面体至少有四个面B.九棱柱有9条侧棱,9个侧面,侧面为平行四边形C.长方体、正方体都是棱柱D.三棱柱的侧面为三角形解析:多面体至少应有四个顶点组成(否则至多3个顶点,而3个顶点只围成一个平面图形),而四个顶点围成四个面,所以A正确;棱柱侧面为平行四边形,其侧棱和侧面的个数与底面多边形的边数相等,所以B正确;长方体、正方体都是棱柱,所以C正确;三棱柱的侧面是平行四边形,不是三角形,所以D错误,故选D.5.长方体的六个面的面积之和为11,十二条棱长度之和为24,则这个长方体的一条对角线的长为(C)A.2B.C.5D.6解析:设长方体的一个顶点上的三条棱的长分别为a、b、c,则,∴(a+b+c)2=36,∴a2+b2+c2=(a+b+c)2-2(ab+bc+ca)=36-11=25,∴对角线长为=5.∴选C.6.下列命题中正确的是(D)A.用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台B.两个底面平行且相似,其余各面都是梯形的多面体是棱台C.侧面都是等腰三角形的棱锥是正棱锥D.棱台的侧棱延长后必交于一点解析:A中,要用“平行于底面”的平面去截棱锥,棱锥底面与截面之间的部分才叫棱台,如果截棱锥的平面不与底面平行,棱锥底面与截面之间的部分只能叫多面体,故A错误;B中,棱台还要求侧棱的延长线交于一点,故B错误;C中,正棱锥还要求底面是正多边形,故C错误;D中,由棱台的定义知,棱台的侧棱延长后必交于一点,故D正确.7.正四棱台两底面的边长分别为a,b,侧面积(侧面展开图的面积)等于两个底面积的和,那么它的高为(A)A.B.C.D.解析:设高为h,斜高为h′, S侧=4×(a+b)h′=2(a+b)h′,S上+S下=a2+b2,又 S侧=S上+S下,∴h′=,∴h===.8.如图,已知正三棱柱ABC-A1B1C1的底面边长为4cm,高为10cm,则一质点自点A出发,沿着三棱柱的侧面,绕行两周到达点A1的最短路线的长为(D)A.16cmB.12cmC.24cmD.26cm解析:将正三棱柱ABC-A1B1C1沿侧棱AA1展开,再拼接一次,其侧面展开图如图所示.在展开图中,最短距离是大矩形对角线的长度,由已知矩形的长等于6×4=24(cm),宽等于10cm,所以最短距离为l==26(cm),故选D.二、填空题9.棱锥的侧棱都相等,所有的侧面上的高也相等,则这个棱锥的底面是正多边形.解析:由侧棱相等知顶点在底面上的射影为底面多边形的外心,又由侧面上高都相等知顶点在底面上的射影为底面多边形的内心,因此底面为正多边形.10.长方体的三个面的面积分别为12,6,8,则长方体的体对角线长为.解析:设长方体的长、宽、高分别为a,b,c,则∴abc=24.分别除以bc,ac,ab,得a=4,b=3,c=2.∴体对角线长为=.11.如图,这是一个正方体的表面展开图,若把它再折回成正方体后,有下列命题:①点H与点C重合;②点D,M,R重合;③点B与点Q重合;④点A与点S重合.其中正确命题的序号是②④(把你认为正确命题的序号都填上).解析:将正方体的六个面分别用“前”“后”“左”“右”“上”“下”标记,若记面NPGF为“下”,面PSRN为“后”,则面PQHG,MNFE,EFCB,DEBA分别为“右”“左”“前”“上”.按各面的标记折成正方体,则点D,M,R重合;点G,C重合;点B,H重合;点A,S,Q...