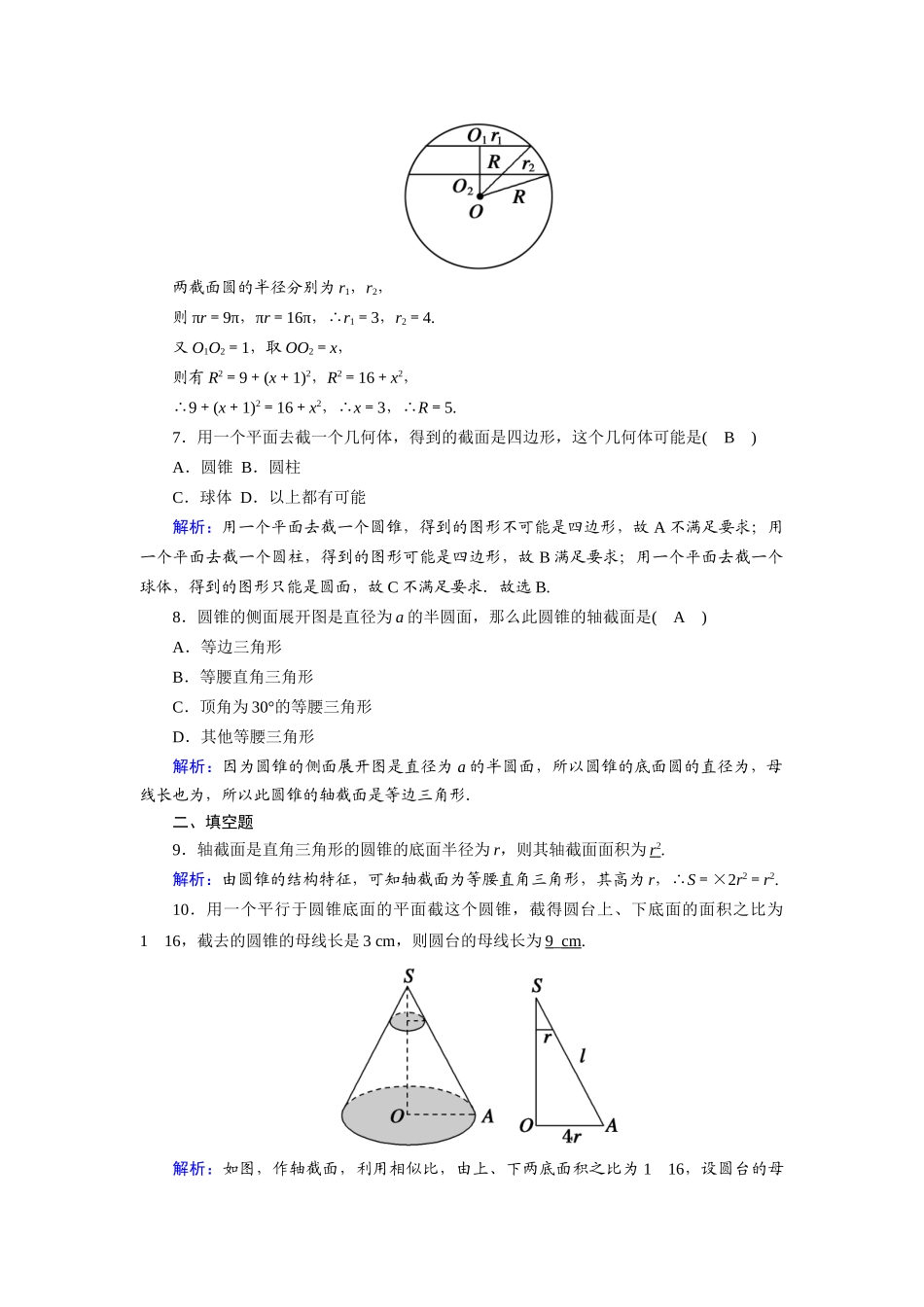
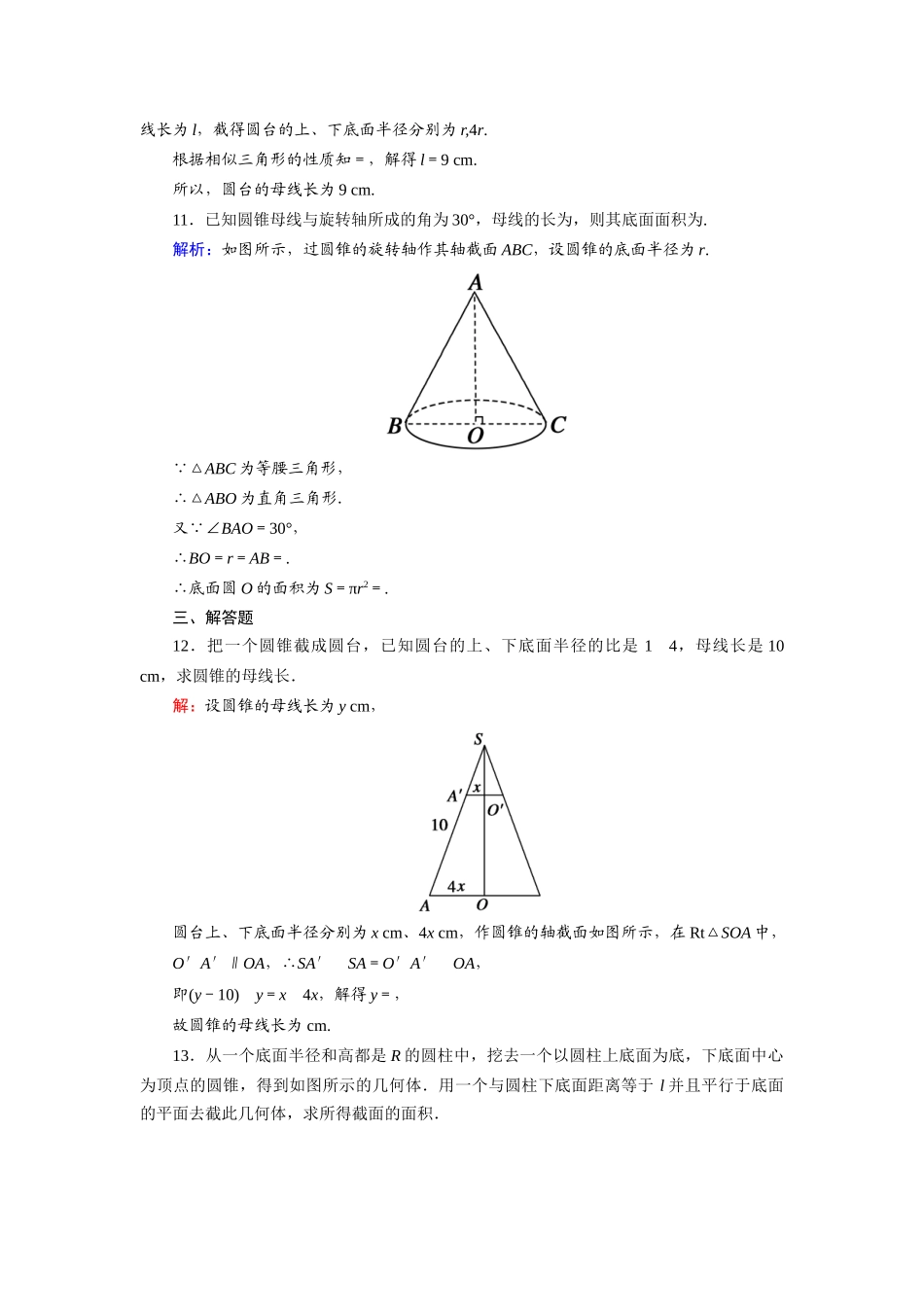
第一章立体几何初步课时作业1简单旋转体时间:45分钟——基础巩固类——一、选择题1.下列几何体中是旋转体的是(D)①圆柱;②六棱锥;③正方体;④球;⑤四面体.A.①和⑤B.①C.③和④D.①和④解析:①圆柱是旋转体;④球是旋转体;②③⑤不是旋转体.2.以矩形的一边所在的直线为旋转轴,其余三边旋转一周形成的面所围成的旋转体是(C)A.球B.圆锥C.圆柱D.圆台解析:根据圆柱的定义,在矩形中,以矩形的一边所在的直线为旋转轴,其余三边旋转形成的面所围成的旋转体是圆柱.3.圆台的所有母线的位置关系是(C)A.平行B.在同一平面内C.延长后交于一点D.垂直解析:圆台是由平行于圆锥底面的截面截圆锥而得到的,所以圆台的母线延长后交于一点.4.以一个等边三角形底边所在的直线为旋转轴旋转一周所得的几何体是(C)A.一个圆柱B.一个圆锥C.两个同底面的圆锥D.一个圆台5.有下列命题:①圆柱的轴截面是过母线的截面中最大的;②用任意一个平面去截球体得到的截面一定是一个圆面;③用任意一个平面去截圆锥得到的截面一定是一个圆.其中正确命题的个数是(C)A.0B.1C.2D.3解析:由圆柱与球的结构特征可知①②正确.故选C.6.已知球的两个平行截面的面积分别为9π和16π,它们位于球心的同一侧,且相距为1,那么这个球的半径是(B)A.4B.5C.3D.3解析:如图,设球的半径为R,两截面圆的半径分别为r1,r2,则πr=9π,πr=16π,∴r1=3,r2=4.又O1O2=1,取OO2=x,则有R2=9+(x+1)2,R2=16+x2,∴9+(x+1)2=16+x2,∴x=3,∴R=5.7.用一个平面去截一个几何体,得到的截面是四边形,这个几何体可能是(B)A.圆锥B.圆柱C.球体D.以上都有可能解析:用一个平面去截一个圆锥,得到的图形不可能是四边形,故A不满足要求;用一个平面去截一个圆柱,得到的图形可能是四边形,故B满足要求;用一个平面去截一个球体,得到的图形只能是圆面,故C不满足要求.故选B.8.圆锥的侧面展开图是直径为a的半圆面,那么此圆锥的轴截面是(A)A.等边三角形B.等腰直角三角形C.顶角为30°的等腰三角形D.其他等腰三角形解析:因为圆锥的侧面展开图是直径为a的半圆面,所以圆锥的底面圆的直径为,母线长也为,所以此圆锥的轴截面是等边三角形.二、填空题9.轴截面是直角三角形的圆锥的底面半径为r,则其轴截面面积为r2.解析:由圆锥的结构特征,可知轴截面为等腰直角三角形,其高为r,∴S=×2r2=r2.10.用一个平行于圆锥底面的平面截这个圆锥,截得圆台上、下底面的面积之比为116,截去的圆锥的母线长是3cm,则圆台的母线长为9_cm.解析:如图,作轴截面,利用相似比,由上、下两底面积之比为116,设圆台的母线长为l,截得圆台的上、下底面半径分别为r,4r.根据相似三角形的性质知=,解得l=9cm.所以,圆台的母线长为9cm.11.已知圆锥母线与旋转轴所成的角为30°,母线的长为,则其底面面积为.解析:如图所示,过圆锥的旋转轴作其轴截面ABC,设圆锥的底面半径为r. △ABC为等腰三角形,∴△ABO为直角三角形.又 ∠BAO=30°,∴BO=r=AB=.∴底面圆O的面积为S=πr2=.三、解答题12.把一个圆锥截成圆台,已知圆台的上、下底面半径的比是14,母线长是10cm,求圆锥的母线长.解:设圆锥的母线长为ycm,圆台上、下底面半径分别为xcm、4xcm,作圆锥的轴截面如图所示,在Rt△SOA中,O′A′∥OA,∴SA′SA=O′A′OA,即(y-10)y=x4x,解得y=,故圆锥的母线长为cm.13.从一个底面半径和高都是R的圆柱中,挖去一个以圆柱上底面为底,下底面中心为顶点的圆锥,得到如图所示的几何体.用一个与圆柱下底面距离等于l并且平行于底面的平面去截此几何体,求所得截面的面积.提示:圆柱中挖去圆锥后的几何体被平行于底面的平面所截得的截面是一个圆环面,它是由圆柱被截得的圆面去掉一个圆锥被截得的同心圆面而得到的,作出轴截面再求解.解:轴截面如图所示.被平行于下底面的平面所截的圆柱的截面圆的半径O1C=R,设圆锥的截面圆的半径O1D为x. OA=AB=R,∴△OAB是等腰直角三角形.又 CD∥OA,∴CD=BC,∴OA-CD=AB-BC,即x=l.∴截面面积S=πR2-πl2=π(R2-l2...