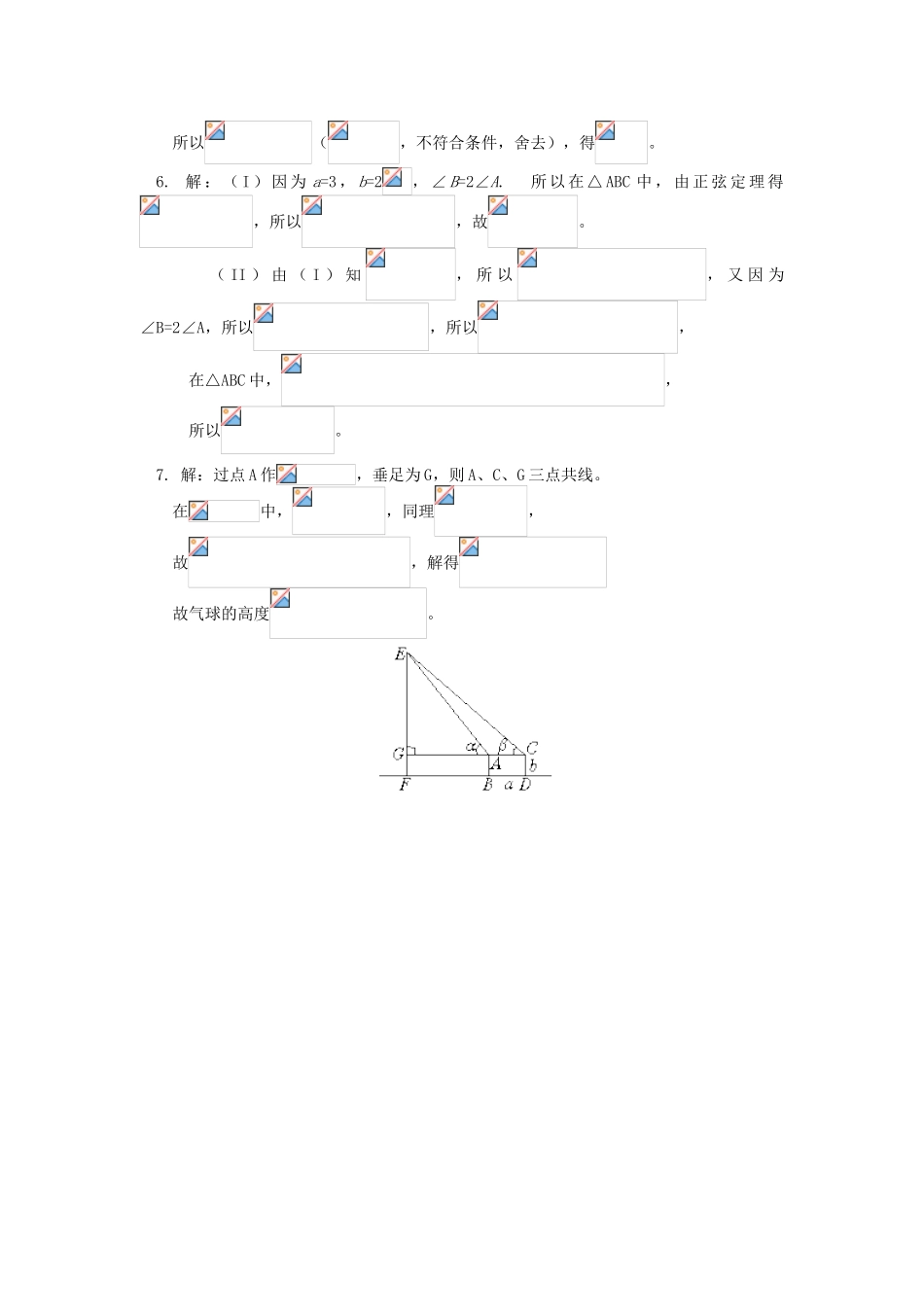
正弦定理、余弦定理的应用(答题时间:40分钟)1.三角形的三边长为连续自然数,且最大角是钝角,那么这个三角形的最小边为。2.(广东高考)在中,角所对应的边分别为,已知,则。3.已知△ABC中,3(+)·=42,则=。4.在△ABC中,a、b、c分别表示三个内角A、B、C的对边,如果(a2+b2)sin(A-B)=(a2-b2)sin(A+B),试判断该三角形的形状。5.在△ABC中,a2+c2=2b2,其中a,b,c分别为角A,B,C所对的边长。(1)求证:B≤;(2)若,且A为钝角,求A。6.(北京高考)在△ABC中,a=3,b=2,∠B=2∠A。(I)求cosA的值;(II)求c的值。7.有两个高度都为b米的两个测角仪AB和CD,水平距离为a米,测得气球E在它们的正西方向的上空仰角分别是是α和β,试用表示出气球的高度。1.解:设三边分别为,由题意得,解得,又,故x=3,最小边为2。2.解:由正弦定理得。3.解:由已知得:,即。—7。4.方法一:∵(a2+b2)sin(A-B)=(a2-b2)sin(A+B)⇔a2[sin(A-B)-sin(A+B)]=b2[-sin(A+B)-sin(A-B)],∴2a2cosAsinB=2b2cosBsinA,由正弦定理,得:sin2AcosAsinB=sin2BcosBsinA,∴sinAsinB(sinAcosA-sinBcosB)=0,∴sin2A=sin2B,由0<2A<2π,0<2B<2π,得2A=2B或2A=π-2B,即△ABC是等腰三角形或直角三角形。方法二:同方法一可得2a2cosAsinB=2b2cosBsinA,由正、余弦定理,即得a2b×=b2a×,∴a2(b2+c2-a2)=b2(a2+c2-b2),即(a2-b2)(c2-a2-b2)=0,∴a=b或c2=a2+b2,∴三角形为等腰三角形或直角三角形。5.(1)证明:由余弦定理,得,因,,由0<B<π,得,命题得证。(2)由正弦定理,得,因,故=1,于是,因为A为钝角,所以。所以(,不符合条件,舍去),得。6.解:(I)因为a=3,b=2,∠B=2∠A.所以在△ABC中,由正弦定理得,所以,故。(II)由(I)知,所以,又因为∠B=2∠A,所以,所以,在△ABC中,,所以。7.解:过点A作,垂足为G,则A、C、G三点共线。在中,,同理,故,解得故气球的高度。