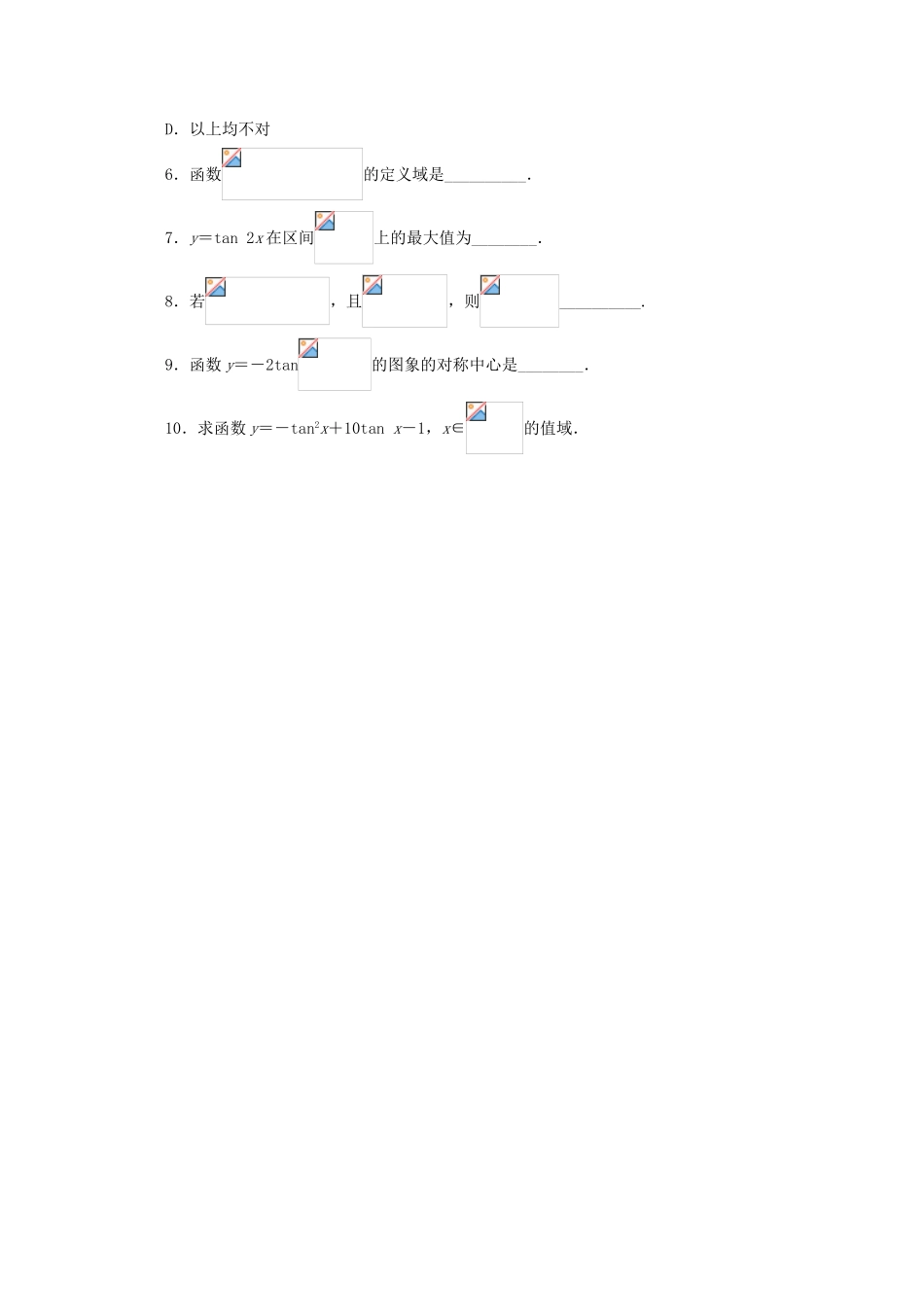
高中数学3.3.2正切函数的图象与性质同步练习湘教版必修21.函数y=cos+tan(π+x)是()A.奇函数B.偶函数C.既是奇函数又是偶函数D.非奇非偶函数2.与函数的图象不相交的直线是()A.B.C.D.3.函数的一个对称中心是()A.B.C.D.4.函数的单调递减区间是()A.(k∈Z)B.(k∈Z)C.(k∈Z)D.(k∈Z)5.y=tan(sinx)的值域为()A.B.C.D.以上均不对6.函数的定义域是__________.7.y=tan2x在区间上的最大值为________.8.若,且,则__________.9.函数y=-2tan的图象的对称中心是________.10.求函数y=-tan2x+10tanx-1,x∈的值域.参考答案1.答案:A解析:y=cos+tan(π+x)=sinx+tanx.定义域为,关于原点对称,且f(-x)=sin(-x)+tan(-x)=-f(x),所以函数是奇函数.2.答案:C解析:∵y=tanx的图象与x=kπ+,k∈Z不相交,∴2x+=kπ+(k∈Z).∴(k∈Z).当k=0时,.3.答案:A解析:令,解得,所以的所有的对称中心坐标是(k∈Z),逐一对照知A正确.4.答案:D解析:由于,所以令,解得2kπ-<x<2kπ+,k∈Z,因此函数的减区间是(k∈Z).5.答案:C解析:当x∈R时,sinx∈.又<-1<1<,∴tan(sinx)∈,即值域为,选C.6.答案:解析:由(k∈Z)得定义域为.7.答案:解析:y=tan2x在区间上是增函数,所以函数的最大值为.8.答案:-m解析:由于f(-x)==-f(x),故f(x)是奇函数,于是.9.答案:解析:由,得(k∈Z).所以函数y=-2tan的图象的对称中心为(k∈Z).10.解:设tanx=t,∵x∈,∴t∈,∴y=-tan2x+10tanx-1=-t2+10t-1=-(t-5)2+24.∴当t=1,即时,ymin=8.当,即时,.∴函数值域为.