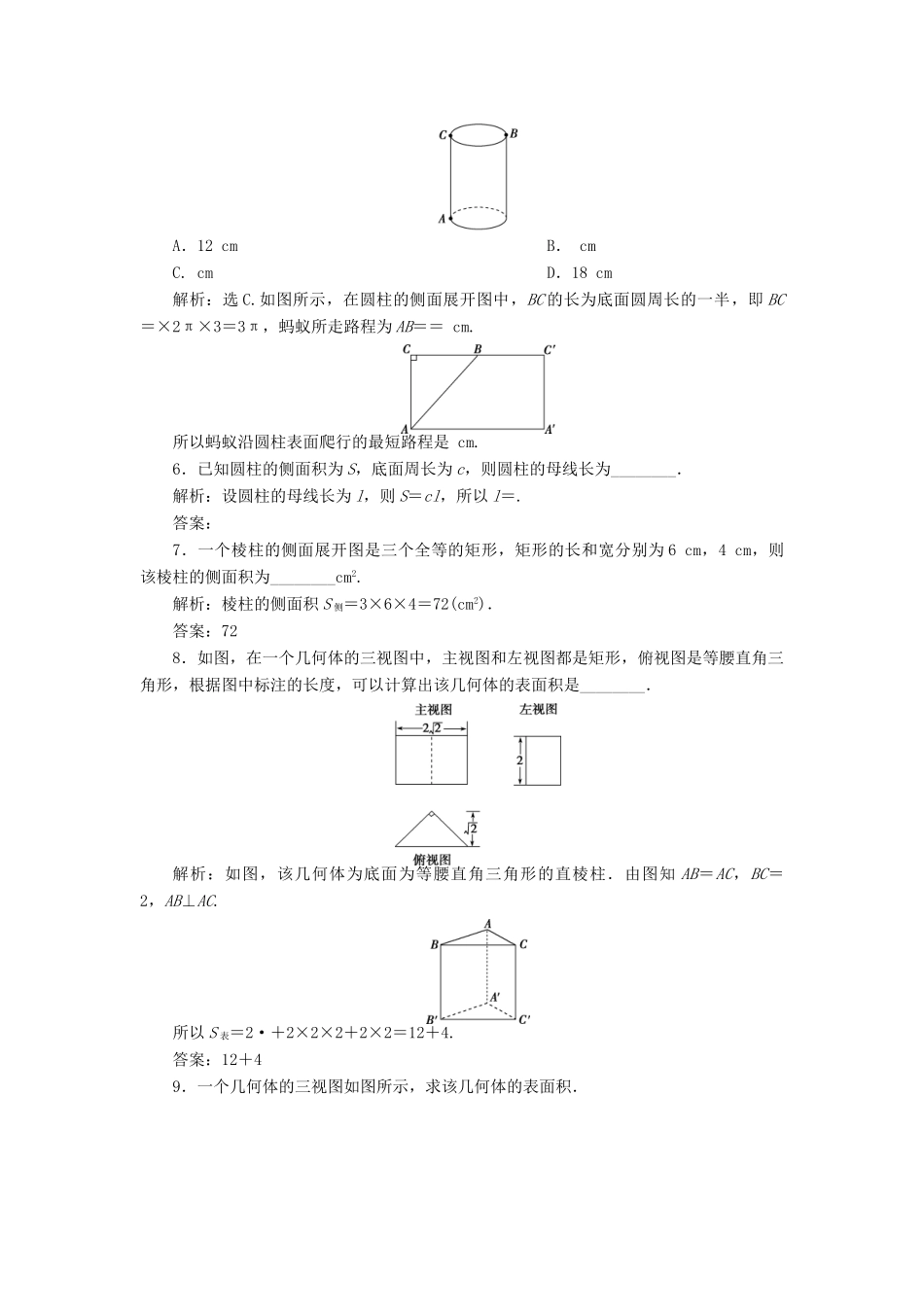
【优化课堂】2016秋高中数学1.7.1柱、锥、台的侧面展开与面积练习北师大版必修2[A基础达标]1.轴截面是正三角形的圆锥称作等边圆锥,则等边圆锥的侧面积是底面积的()A.4倍B.3倍C.倍D.2倍解析:选D.设轴截面正三角形的边长为2a,所以S底=πa2,S侧=πa×2a=2πa2,所以S侧=2S底.2.轴截面为正方形的圆柱的侧面积与表面积的比是()A.1∶2B.2∶3C.1∶3D.1∶4解析:选B.设圆柱的底面半径为r,母线长为l,依题意得l=2r,而S侧面积=2πrl,S表面积=2πr2+2πrl,所以S侧面积∶S表面积=2πrl∶(2πr2+2πrl)=2∶3,故选B.3.圆台OO′的母线长为6,两底面半径分别为2,7,则圆台OO′的侧面积是()A.54πB.8πC.4πD.16π解析:选A.S圆台侧=π(r+r′)l=π(7+2)×6=54π.4.若一个几何体的三视图如图所示,则这个几何体的侧面积为()A.8+B.5+C.5+2D.4+解析:选B.由三视图可知该几何体是一个直四棱柱,底面是一个直角梯形,不垂直于底边的腰长为=,于是侧面积S侧=(1+2+2+)×1=5+.5.如图所示,有一个圆柱,在圆柱下底面的点A处有一只蚂蚁,它想吃到上底面的点B处的食物.当圆柱的高等于12cm,底面半径为3cm时,蚂蚁沿圆柱表面爬行的最短路程是()A.12cmB.cmC.cmD.18cm解析:选C.如图所示,在圆柱的侧面展开图中,BC的长为底面圆周长的一半,即BC=×2π×3=3π,蚂蚁所走路程为AB==cm.所以蚂蚁沿圆柱表面爬行的最短路程是cm.6.已知圆柱的侧面积为S,底面周长为c,则圆柱的母线长为________.解析:设圆柱的母线长为l,则S=cl,所以l=.答案:7.一个棱柱的侧面展开图是三个全等的矩形,矩形的长和宽分别为6cm,4cm,则该棱柱的侧面积为________cm2.解析:棱柱的侧面积S侧=3×6×4=72(cm2).答案:728.如图,在一个几何体的三视图中,主视图和左视图都是矩形,俯视图是等腰直角三角形,根据图中标注的长度,可以计算出该几何体的表面积是________.解析:如图,该几何体为底面为等腰直角三角形的直棱柱.由图知AB=AC,BC=2,AB⊥AC.所以S表=2·+2×2×2+2×2=12+4.答案:12+49.一个几何体的三视图如图所示,求该几何体的表面积.解:由几何体的三视图知这个几何体是一个下面是长方体,上面是圆锥的简单组合体,长方体底面长为3,宽为2,高为1,圆锥底面半径为1高为3,母线长为,表面积为:S=πrl+2(2×1+2×3+1×3)-πr2=π×1×+22-π=22+(-1)π.10.已知正三棱锥VABC的主视图、俯视图如图所示,其中VA=4,AC=2,求该三棱锥的表面积.解:由主视图与俯视图可得正三棱锥的直观图(如图),且VA=VB=VC=4,AB=BC=AC=2.取BC的中点D,连接VD,则VD⊥BC,有VD===,则S△VBC=×VD×BC=××2=,S△ABC=×(2)2×=3,所以,三棱锥VABC的表面积为3S△VBC+S△ABC=3+3=3(+).[B能力提升]1.在一个长方体上钻一个圆柱形的孔,则钻孔后得到的几何体的表面积与原几何体相比()A.变大了B.变小了C.相等D.不确定解析:选D.所得几何体的表面积为长方体的表面积减去两个圆柱底面积,再加上圆柱侧面积,由于长方体形状不确定,钻去的圆柱形状不确定,因此圆柱的两底面积和侧面积不确定,故选D.2.过圆锥的高的三等分点作平行于底面的截面,它们把圆锥的侧面分成的三部分的面积之比为________.解析:如图,由题意知O1A1∶O2A2∶OA=1∶2∶3,以O1A1,O2A2,OA为底面半径的圆锥的侧面积之比为1∶4∶9.故圆锥被截面分成的三部分侧面的面积之比为1∶(4-1)∶(9-4)=1∶3∶5.答案:1∶3∶53.一个正四棱台上、下两底面边长分别为m、n,侧面积等于两个底面面积之和,求这个棱台的高.解:如图,设O1、O分别为棱台上、下底面中心,M1、M分别为B1C1、BC的中点,连接O1O、M1M、O1M1、OM,则M1M为斜高.过M1作M1H⊥OM于H点,则M1H=OO1,S侧=4×(m+n)·M1M,S上底+S下底=m2+n2.由已知得2(m+n)M1M=m2+n2,所以M1M=.在Rt△M1HM中,MH=OM-O1M1=(n-m),所以M1H=O1O===.4.(选做题)有一塔形几何体由3个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点.已知最底层正方...