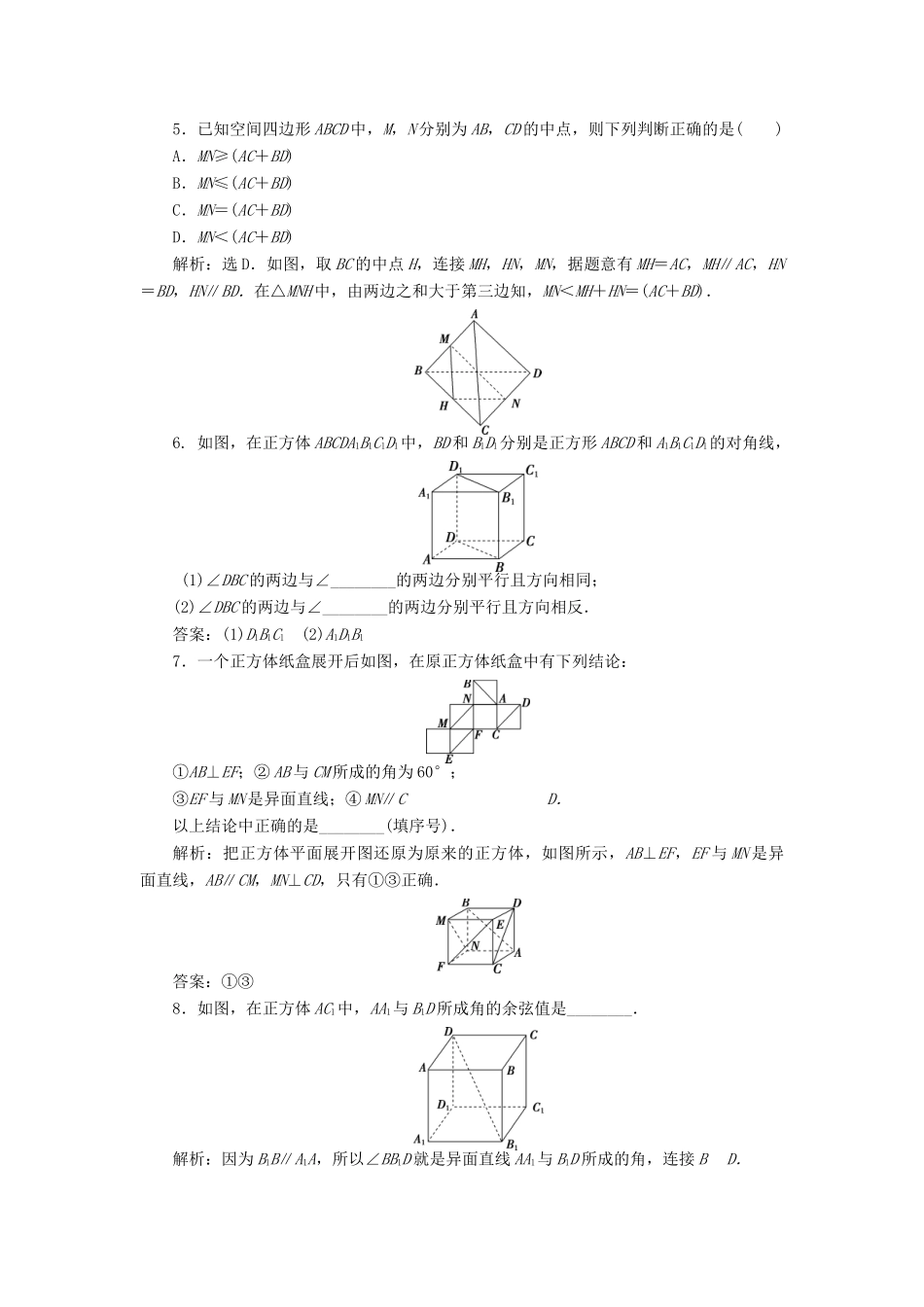
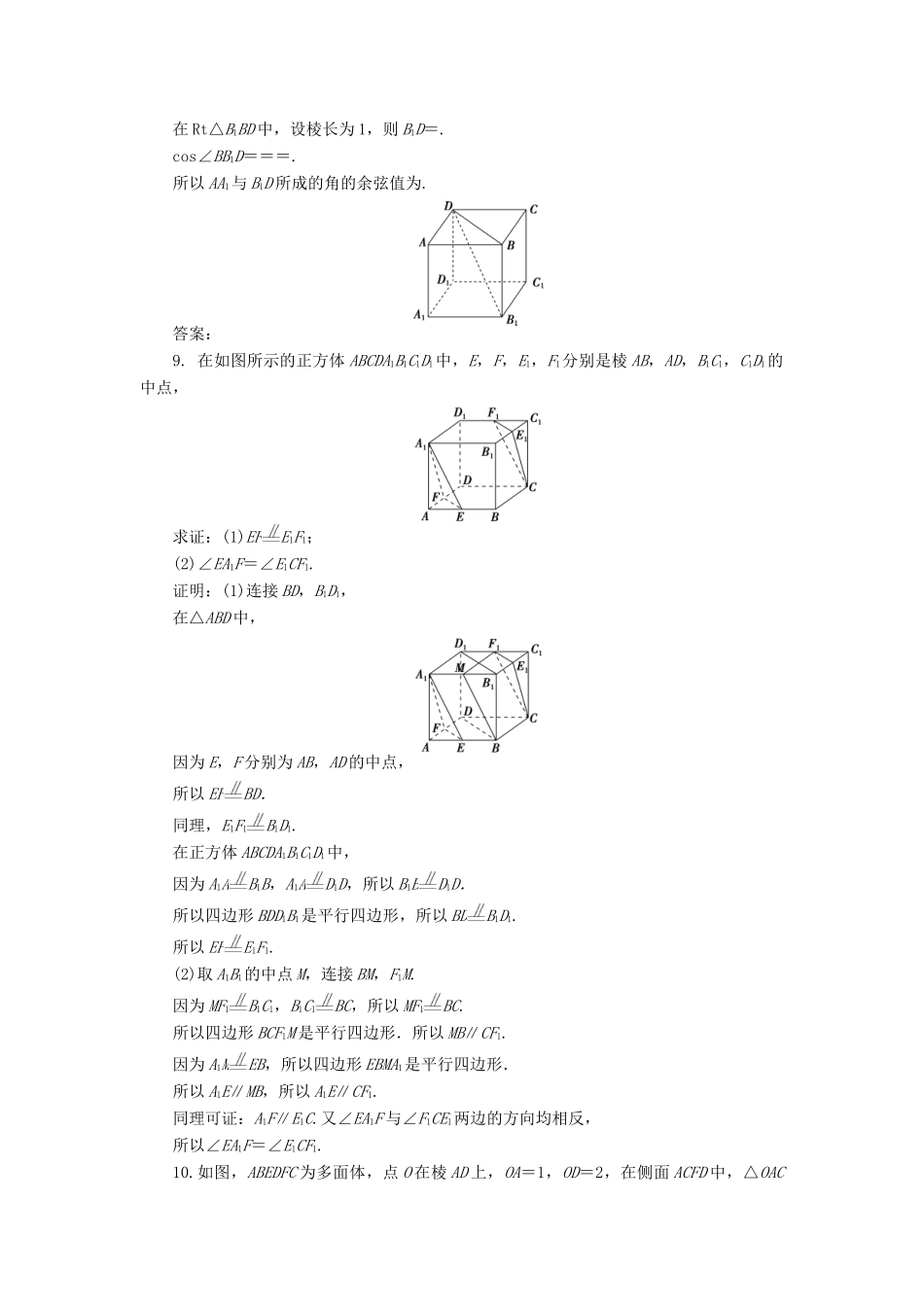
【优化课堂】2016秋高中数学1.4.2空间图形的公理(二)练习北师大版必修2[A基础达标]1.下列命题中,真命题的个数是()①如果一个角的两边与另一个角的两边分别平行,那么这两个角相等;②如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角或直角相等;③如果一个角的两边和另一个角的两边分别垂直,那么这两个角相等或互补.A.0B.1C.2D.3解析:选B.①这两个角也可能互补,故①是错误的;②是正确的,它是等角定理的推广和延伸.③空间两条直线的垂直包括异面垂直,此时两个角有可能不相等且不互补,故③是错误的.所以结论正确的个数为1.2.已知不同的直线a,b,c,下列说法正确的是()A.a∥b,b∥c,则a∥cB.a与b异面,b与c异面,则a与c异面C.a与b相交,b与c相交,则a与c相交D.a与b所成的角与b与c所成的角相等,则a∥c解析:选A.A是公理4的内容.如图正方体中,AB,A1B1都与CC1异面,但AB与A1B1不异面,B错,AB,A1B1都与BB1相交,但AB与A1B1不相交,C错;AB,BC都与DD1成90°角,但AB与BC不平行,D错.3.两个三角形不在同一平面内,它们的边两两对应平行,那么这两个三角形()A.全等B.相似C.仅有一个角相等D.全等或相似解析:选D.由等角定理知,这两个三角形的三个角分别对应相等,所以选D.4.一条直线与两条平行线中的一条为异面直线,则它与另一条()A.相交B.异面C.相交或异面D.平行解析:选C.如图所示的长方体ABCDA1B1C1D1中,直线AA1与直线B1C1是异面直线,与B1C1平行的直线有A1D1,AD,BC,显然直线AA1与A1D1相交,与BC异面.5.已知空间四边形ABCD中,M,N分别为AB,CD的中点,则下列判断正确的是()A.MN≥(AC+BD)B.MN≤(AC+BD)C.MN=(AC+BD)D.MN<(AC+BD)解析:选D.如图,取BC的中点H,连接MH,HN,MN,据题意有MH=AC,MH∥AC,HN=BD,HN∥BD.在△MNH中,由两边之和大于第三边知,MN<MH+HN=(AC+BD).6.如图,在正方体ABCDA1B1C1D1中,BD和B1D1分别是正方形ABCD和A1B1C1D1的对角线,(1)∠DBC的两边与∠________的两边分别平行且方向相同;(2)∠DBC的两边与∠________的两边分别平行且方向相反.答案:(1)D1B1C1(2)A1D1B17.一个正方体纸盒展开后如图,在原正方体纸盒中有下列结论:①AB⊥EF;②AB与CM所成的角为60°;③EF与MN是异面直线;④MN∥CD.以上结论中正确的是________(填序号).解析:把正方体平面展开图还原为原来的正方体,如图所示,AB⊥EF,EF与MN是异面直线,AB∥CM,MN⊥CD,只有①③正确.答案:①③8.如图,在正方体AC1中,AA1与B1D所成角的余弦值是________.解析:因为B1B∥A1A,所以∠BB1D就是异面直线AA1与B1D所成的角,连接BD.在Rt△B1BD中,设棱长为1,则B1D=.cos∠BB1D===.所以AA1与B1D所成的角的余弦值为.答案:9.在如图所示的正方体ABCDA1B1C1D1中,E,F,E1,F1分别是棱AB,AD,B1C1,C1D1的中点,求证:(1)EFE1F1;(2)∠EA1F=∠E1CF1.证明:(1)连接BD,B1D1,在△ABD中,因为E,F分别为AB,AD的中点,所以EFBD.同理,E1F1B1D1.在正方体ABCDA1B1C1D1中,因为A1AB1B,A1AD1D,所以B1BD1D.所以四边形BDD1B1是平行四边形,所以BDB1D1.所以EFE1F1.(2)取A1B1的中点M,连接BM,F1M.因为MF1B1C1,B1C1BC,所以MF1BC.所以四边形BCF1M是平行四边形.所以MB∥CF1.因为A1MEB,所以四边形EBMA1是平行四边形.所以A1E∥MB,所以A1E∥CF1.同理可证:A1F∥E1C.又∠EA1F与∠F1CE1两边的方向均相反,所以∠EA1F=∠E1CF1.10.如图,ABEDFC为多面体,点O在棱AD上,OA=1,OD=2,在侧面ACFD中,△OAC和△ODF为正三角形,在底面ABED中,△OAB和△ODE也都是正三角形,求证:直线BC∥EF.证明:设G是线段DA与线段EB延长线的交点,由于△OAB与△ODE都是正三角形,所以OB∥DE,OB=DE,所以OG=OD=2.同理,设G′是线段DA与线段FC延长线的交点,有OG′=OD=2,又由于G与G′都在线段DA的延长线上,所以G与G′重合,在△GED和△GFD中,由OB∥DE,OB=DE和OC∥DF,OC=DF,可知B,C分别是GE,GF的中点,所以BC是△GFE的中位线,故BC∥EF.[B能力提升]1.已知在四面体ABCD中,E,F分别是AC,BD的中点,若AB=2...