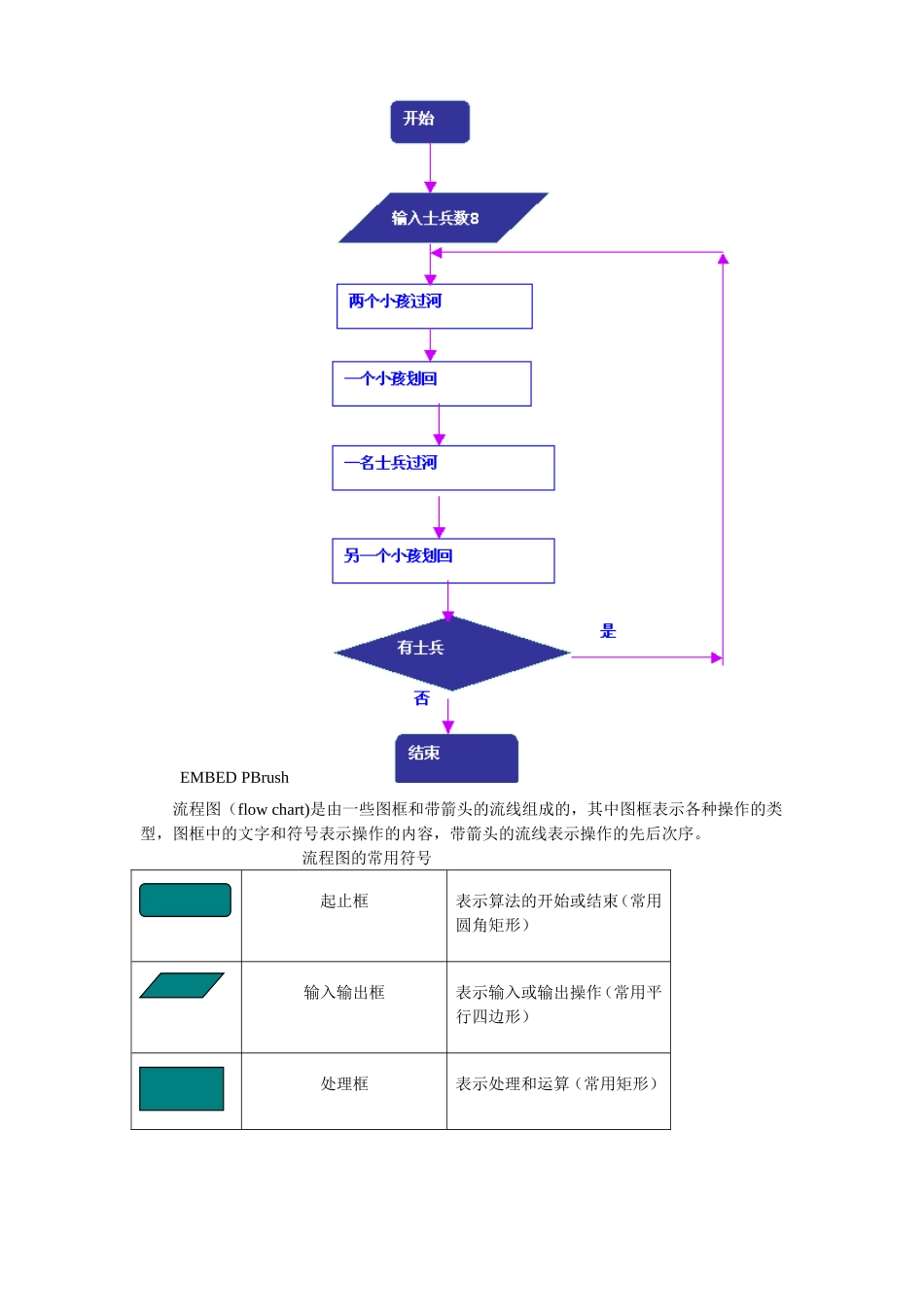
高一数学算法初步一.本周教学内容:算法初步二、本周教学目标1、通过实例体会算法的思想,了解算法的含义;能按步骤用自然语言写出简单问题的算法过程;并了解算法的主要特点。2、了解常用流程图符号(输入输出框,处理框,判断框,起止框,流线等)的意义。能用流程图表示顺序、选择、循环这三种基本结构。3、能识别简单流程图所描述的算法。三、本周知识要点1、算法的含义一般而言,对一类问题的机械的、统一的求解方法称为算法。注意:算法不同于求解一个具体问题的方法,它有如下的要求:(1)写出的算法,必须能解决一类问题,并且能重复使用;(2)算法过程要能一步步执行,每一步执行的操作,必须确切,不能含混不清,而且在有限步后能得出问题的答案或指出问题没有解答。2、算法的基本特征:(1)有限性一个算法在执行有限个步骤后必须结束。事实上,“有限性”往往指“在合理的范围内”。如果让计算机执行一个历时1000年才能结束的算法,即使有限,也不能视为有效算法,因为它超出了合理的范围。“合理限度”一般由人们的常识和需要而定。(2)确定性算法的每一个步骤和次序都应当是确定的。即不能含糊不清、模棱两可、或者被解释成不同的含义。例如,一个健身操中的一个动作“手举过头顶”是不确定的,含糊的。也就是说,算法的含义应当唯一,而不能产生“歧义性”,即被理解为两种或者两种以上的含义。2、流程图情景:某部士兵有8个人要过河,岸边只有一只小船,两个小孩,士兵和小孩都会划船,但小船一次只能乘一个士兵或两个小孩,请你设计一种算法,让这8个士兵过河到河对岸。算法:S1两个小孩过河;S2一个小孩上岸,另一个小孩划船回原岸;S3一个士兵划船过河到对岸;S4小孩划船回到原岸;S5如果还有士兵,转到S1重复操作;如果没有士兵,结束。EMBEDPBrush流程图(flowchart)是由一些图框和带箭头的流线组成的,其中图框表示各种操作的类型,图框中的文字和符号表示操作的内容,带箭头的流线表示操作的先后次序。流程图的常用符号起止框表示算法的开始或结束(常用圆角矩形)输入输出框表示输入或输出操作(常用平行四边形)处理框表示处理和运算(常用矩形)判断框根据条件决定执行两条路径中的某一条(常用菱形)流程线表示执行步骤的路径(常用箭头线)3、流程图的三种逻辑结构(1)顺序结构:是算法的操作顺序,是按照书写顺序执行的,这是任何一个算法必有的基本结构,是最简单的算法结构。(2)先根据条件作出判断,再决定执行哪一种操作的结构称为选择结构(或称为“分支结构”)。如图,虚线框内是一个选择结构,它包含一个判断框,当条件P成立(或称为“真”)时执行A,否则执行B。EMBEDPBrush(3)在算法中,像这种需要重复执行同一操作的结构称为循环结构(cyclestructure)。如图就是一种常见的循环结构:先执行A框,再判断所给条件P的真假;若P为“假”,则再执行A框,如此反复,直到P为“真”,该循环过程结束。【典型例题】例1.给出求1+2+3+4+5的一个算法算法1按照逐一相加的程序进行第一步计算1+2,得到3;第二步将第一步中的运算结果3与3相加,得到6;第三步将第二步中的运算结果6与4相加,得到10;第四步将第三步中的运算结果10与5相加,得到15。算法2可以运用公式直接计算第一步取第二步计算第三步输出运算结果例2.给出求解方程组的一个算法我们用消元法求解这个个方程组:第一步方程(1)不动,将方程(2)中x的系数除以方程(1)中x的系数,得到乘数m=第二步方程(2)减去m乘以方程(1),消去方程(2)中的x项,得到第三步将上面方程组自上而下回代求解,得到y=-1,x=4这种消元回代的算法适用于一般线性方程组的求解。例3.已知两个单元分别存放了变量x和y的值,试交换这两个变量值。解:为了达到交换的目的,需要一个单元存放中间变量p其算法是:例4.设计求解一元二次方程的一个算法,并用流程图表示。分析:因为一元二次方程未必总有实数根,故求解时先计算判别式,然后比较判别式与0的大小,再决定能否用求根公式进行求解。因此,在算法中应含有选择结构。算法如下:根据上述步骤,算法流程图为EMBEDPBrush例5.写出求1×2×3×4×5...