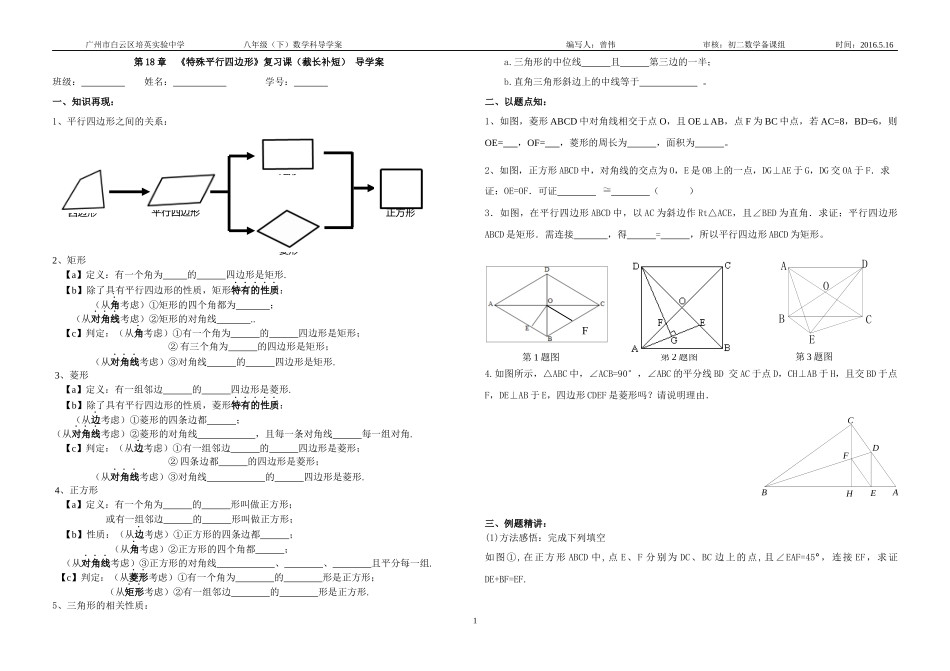
DACFHEB四边形平行四边形菱形矩形正方形F广州市白云区培英实验中学八年级(下)数学科导学案编写人:曾伟审核:初二数学备课组时间:2016.5.16第18章《特殊平行四边形》复习课(截长补短)导学案班级:姓名:学号:一、知识再现:1、平行四边形之间的关系:2、矩形【a】定义:有一个角为的四边形是矩形.【b】除了具有平行四边形的性质,矩形特有的性质:(从角考虑)①矩形的四个角都为;(从对角线考虑)②矩形的对角线..【c】判定:(从角考虑)①有一个角为的四边形是矩形;②有三个角为的四边形是矩形;(从对角线考虑)③对角线的四边形是矩形.3、菱形【a】定义:有一组邻边的四边形是菱形.【b】除了具有平行四边形的性质,菱形特有的性质:(从边考虑)①菱形的四条边都;(从对角线考虑)②菱形的对角线,且每一条对角线每一组对角.【c】判定:(从边考虑)①有一组邻边的四边形是菱形;②四条边都的四边形是菱形;(从对角线考虑)③对角线的四边形是菱形.4、正方形【a】定义:有一个角为的形叫做正方形;或有一组邻边的形叫做正方形;【b】性质:(从边考虑)①正方形的四条边都;(从角考虑)②正方形的四个角都;(从对角线考虑)③正方形的对角线、、且平分每一组.【c】判定:(从菱形考虑)①有一个角为的形是正方形;(从矩形考虑)②有一组邻边的形是正方形.5、三角形的相关性质:a.三角形的中位线且第三边的一半;b.直角三角形斜边上的中线等于。二、以题点知:1、如图,菱形ABCD中对角线相交于点O,且OEAB⊥,点F为BC中点,若AC=8,BD=6,则OE=,OF=,菱形的周长为,面积为。2、如图,正方形ABCD中,对角线的交点为O,E是OB上的一点,DG⊥AE于G,DG交OA于F.求证:OE=OF.可证()3.如图,在平行四边形ABCD中,以AC为斜边作Rt△ACE,且∠BED为直角.求证:平行四边形ABCD是矩形.需连接,得=,所以平行四边形ABCD为矩形。4.如图所示,△ABC中,∠ACB=90°,∠ABC的平分线BD交AC于点D,CH⊥AB于H,且交BD于点F,DE⊥AB于E,四边形CDEF是菱形吗?请说明理由.三、例题精讲:(1)方法感悟:完成下列填空如图①,在正方形ABCD中,点E、F分别为DC、BC边上的点,且∠EAF=45°,连接EF,求证DE+BF=EF.第2题图第1题图第3题图BACEDO1广州市白云区培英实验中学八年级(下)数学科导学案编写人:曾伟审核:初二数学备课组时间:2016.5.16证明:延长FB至点G,使得BG=DE,连接AG。在正方形ABCD中,AB=AD,=∠D=90°∵∠ABG=180°−=∴∠=∠在△ABG与△ADE中∴∠1=∠2,AG=AE.∵∠2+∠EAF+∠3=90°∴∠1+∠EAF+∠3=90°即∠EAF+∠______=90°∴∠=90°-∠EAF=∴∠=∠EAF在△AFG与△AFE中∴FG=EF又FG=GB+BF=DE+BF∴DE+BF=EF(2)变式训练:如图①,在正方形ABCD中,点E,F分别为DC,BC边上的点,DE+BF=EF,连接EF,求证∠EAF=45°.(3)方法迁移:如图②,将Rt△ABC沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想。(4)问题拓展:如图③,在四边形ABCD中,AB=AD,E,F分别为DC,BC上的点,满足∠EAF=∠DAB,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF.请直接写出你的猜想(不必说明理由).四、课堂训练:1、如图,正方形ABCD的边长为1,点M、N分别在BC、CD上,使得△CMN的周长为2.求:∠MAN的大小。2EFDCABABCDADBCE广州市白云区培英实验中学八年级(下)数学科导学案编写人:曾伟审核:初二数学备课组时间:2016.5.162、正方形ABCD中,点E在CD延长线上,点F在BC延长线上,EAF=45°,求证:EF=BF-DE3、如图,ABCD是正方形,∠FAD=∠FAE.请问DF、AE、BE又有什么数量关系?.五、总结提升:六、强化训练:1、如图,在四边形ABCD中,BC>AB,AD=DC,BD平分∠ABC.求证:∠BAD+∠BCD=180°.2、如图,AD∥BC,点E在线段AB上,∠ADE=∠CDE,∠DCE=∠ECB.求证:CD=AD+BC.3、五边形ABCDE中,AB=AE,BC+DE=CD,∠ABC+∠AED=180°,求证:AD平分∠CDEFEDCBACEDBA3广州市白云区培英实验中学八年级(下)数学科导学案编写人:曾伟审核:初二数学备课组时间:2016.5.164