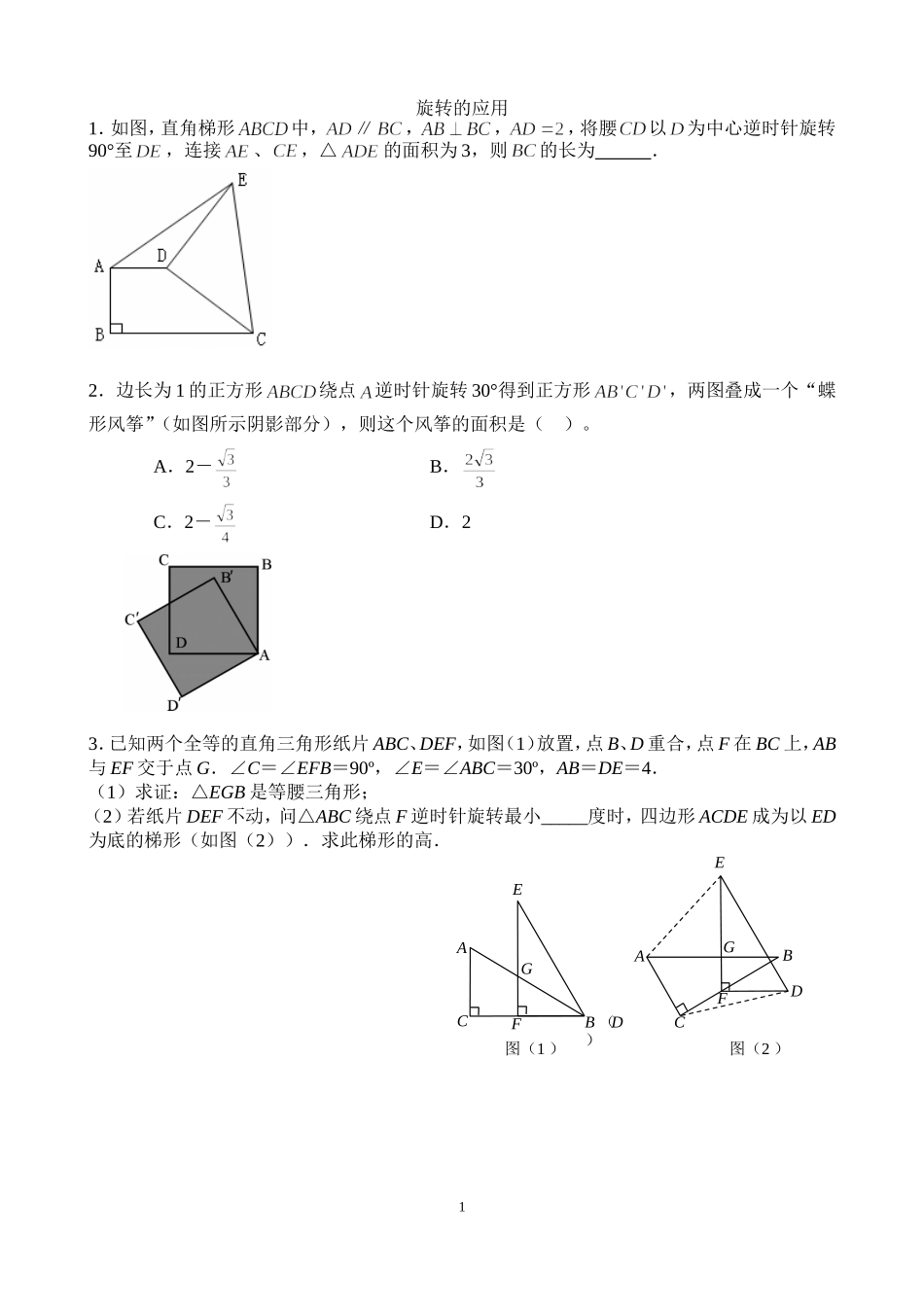
旋转的应用1.如图,直角梯形中,∥,,,将腰以为中心逆时针旋转90°至,连接、,△的面积为3,则的长为.2.边长为1的正方形绕点逆时针旋转30°得到正方形,两图叠成一个“蝶形风筝”(如图所示阴影部分),则这个风筝的面积是()。A.2-B.C.2-D.23.已知两个全等的直角三角形纸片ABC、DEF,如图(1)放置,点B、D重合,点F在BC上,AB与EF交于点G.∠C=∠EFB=90º,∠E=∠ABC=30º,AB=DE=4.(1)求证:△EGB是等腰三角形;(2)若纸片DEF不动,问△ABC绕点F逆时针旋转最小_____度时,四边形ACDE成为以ED为底的梯形(如图(2)).求此梯形的高.1图(1)ABCEFFB(D)GGACED图(2)4.如图1,已知正方形ABCD的边CD在正方形DEFG的边DE上,连接AE,GC.(1)试猜想AE与GC有怎样的位置关系,并证明你的结论;(2)将正方形DEFG绕点D按顺时针方向旋转,使点E落在BC边上,如图2,连接AE和GC.你认为(1)中的结论是否还成立?若成立,给出证明;若不成立,请说明理由.5.如图1,在△中,点为边中点,直线绕顶点旋转,若点、在直线的异侧,⊥直线于点,⊥直线于点,连接、。(1)延长交于点(如图2)。①求证:△≌△;②;(2)若直线绕点旋转到图3的位置时,点、在直线的同侧,其它条件不变,此时成立吗?若成立,请给予证明,若不成立,请说明理由;(3)若直线绕点旋转到与边平行的位置时,其它条件不变。请直接判断四边形的形状及此时还成立吗?不必说明理由.2aABCPMNABCMNaPABCPNMa图1图2图36.如图1,已知矩形,点是边的中点,且.(1)判断△的形状,并说明理由;(2)保持图1中的△固定不变,绕点旋转所在的直线到图2中的位置(当垂线段、在直线的同侧).试探究线段、、长度之间有什么关系?并给予证明;(3)保持图2中的△固定不变,继续绕点旋转所在的直线到图3中的位置(当垂线段、在直线的异侧).试探究线段、、长度之间有什么关系?并给予证明.EDCBA图1EDCBA图2MNNM图3ABCDE7.如图1,在△中,,为边上一点,连接,以、为邻边作□,与相交于点,已知.(1)求证:;(2)□是否为矩形?请说明理由;(3)如图2,为中点,连接,将∠绕点顺时针旋转适当的角度,得到∠(点、分别是∠的两边与、延长线的交点).猜想线段与之间的数量关系,并证明你的结论.3图1ABDCEP图2ABDCEPMNF8.在Rt△ABC中,∠BAC=90°,∠B=30°,线段AD是BC边上的中线,如图①,将△ADC沿直线BC平移,使点D与点C重合,得到△FCE,如图②,再将△FCE绕点C顺时针旋转,设旋转角为,连接AF、DE。(1)在旋转过程中,当∠ACE=150°时,求旋转角的度数;(2)探究旋转过程中四边形ADEF能形成那些特殊四边形?请说明理由.4ABCDEF图①图②ABDCFEABCD备用图ABCD备用图9.如图,已知正方形OABC在直角坐标系xoy中,点A、C分别在x、y轴的正半轴上,点O为坐标原点,等腰直角三角板OEF的直角顶点O在坐标原点,E、F分别在OA、OC上,且OA=4,OE=2,将三角板OEF绕O点逆时针旋转至OE1F1,的位置,连接AE1、CF1.(1)求证:△AOE1≌△OCF1;(2)将三角板OEF绕O点逆时针旋转一周,是否存在某一位置,使得OE∥CF,若存在,请求出此时E点的坐标,若不存在,请说明理由.10.如图,四边形是正方形,△是等边三角形,为对角线(不含点)上任意一点,将绕点逆时针旋转60°得到,连接、、.⑴求证:△≌△;⑵①当点在何处时,的值最小;②当点在何处时,的值最小,并说明理由;⑶当的最小值为时,求正方形的边长.5ABCFOxEE1F1yEADBCNM11.如图1,已知∠ABC=90°,△ABE是等边三角形,点P为射线BC上任意一点(点P与点B不重合),连结AP,将线段AP绕点A逆时针旋转60°得到线段AQ,连结QE并延长交射线BC于点F.(1)如图2,当BP=BA时,∠EBF=°,猜想∠QFC=°;(2)如图1,当点P为射线BC上任意一点时,猜想∠QFC的度数,并加以证明;(3)已知线段AB=32,设BP=x,点Q到射线BC的距离为y,求y关于x的函数关系式.12.我们容易发现:反比例函数的图象是一个中心对称图形.可以利用这一结论解决问题.如图,在同一直角坐标系中,正比例函数的图象可以看作是:将轴所在的直线绕着原点逆时针旋转度角后的图形.若它与反比例函数...