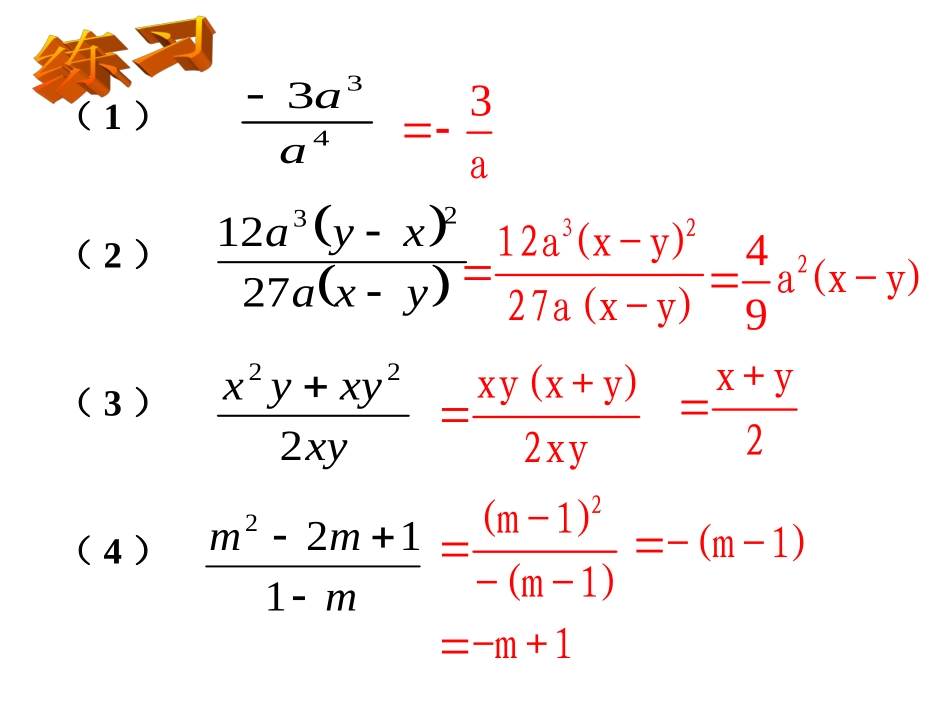分式的乘法和除法VIP免费

mmm1122433aaxyxyyx222yxaxya271223（1）（2）（3）（4）a3212a(x-y)27a(x-y)492a(x-y)xy(x+y)2xyx+y22(m-1)-(m-1)-(m-1)-m+1232()58()aababa22276xxxx2621xyyxx222228xxyyxyxy232()8()aabaab14()ab2(1)(1)yxx1yx(1)(2)(3)(2)xxxx13xx2()()xyxyxyxyxy知识回顾1.根据分数的乘除法则计算:14972673642312.请你根据你的猜想填空:类似的法则可以推广到分式的乘除运算中去吗?为什么?=÷abdc=bcadbdacbdac··bdacbacd探究即结合(1)(2)两题思考:分式的乘除法法则?分式乘分式，用分子的积做积的分子，分母的积做积的分母；分式除以分式，把除式的分子、分母颠倒位置后，与被除式相乘。acbdacbd÷adbcadbc=acbd注：这里的字母a、b、c、d可以表示任何整式，但字母的取值不能使分母为零。整式与分式运算时，可以把整式看成分母是1的式子。例1、计算：;aa3227b67b(1)aa2b23b(2)÷(-);解：aa3227b67b(1)aa3227b67b4.3abaa2b23b(2)÷(-)=aa2b2(-)=3baa2b2-3b2.3a2-b分子和分母都是单项式的分式乘除法的解题步骤是：①把分式除法运算变成分式乘法运算；②求积的分式，确定积的符号；③约分。你是否悟到了怎么去做此类分式的乘除法运算?④分式运算的结果通常要化成最简分式或整式。动手试一试232xy-3xy292xy3ab229aaaaaaa222-4(3)÷-6-322aaaaaaa()(-3)(-3)(2)(-2)22.6aaa-51622m-(4)÷(m+4m)12-3m(m+4)(m-4)3(4-m)m(m+4)1-3m计算时该注意什么：计算时该注意什么：1.1.先定符号先定符号3.3.先“分”后“约”先“分”后“约”2.2.化除为乘化除为乘2(3)(2)aaa•分子或分母是多项式的分式乘除法的解题步骤是•①除法转化为乘法；•②把各分式中分子或分母里的多项式分解因式；•③约分得到积的分式例2计算：（1）222441214aaaaaa解：（1）222441214aaaaaa22(2)1(1)(2)(2)aaaaa2(1)(2)aaa22(2)(1)(1)(2)(2)aaaaa(2)2211497mmm2222114971(7)49mmmmmm解:(7)(7)(7)mmmm7mm•课堂练习2)1(abba21abbaa21()aaaa解1))(2(2aaaa2211)3(yxyx2()(1)aaaa(1)(1)aaaa221aa2211xyyx解(1)(1)(1)xxyyyxxyy1、下面的计算对吗？若不对，应该怎样改正？xxbbx362)1(232234)2(xaaxxyyx1)3(（错。应改为：）x3（错。应改为：）（错。应改为：）2238ax2yx222))(4(abababab（对）辨一辨3aaa1D、a13x13C、x12m2m1B、1baabA、）的是（2、下列计算中，正确D3、计算:xyxyxxy2-(1)(-)÷();4111.12xxxxxx22(2)÷-解:原式xyxxxy(y-)()-xy2=-解:原式2111xxxxxxx()(2-1)()=()-(2-1)21x-()21x=--4、计算：2(1);23baxaaxb6-b÷×22(2).41xxxxx-4-1÷2例3、一个长、宽、高分别为l，b，h的长方形纸箱装满了一层高为h的圆柱形易拉罐（如图）.求纸箱空间的利用率（易拉罐总体积与纸箱容积的比，结果精确到1%）.rlb解：由题意得，易拉罐的总数为2422rlbrbrl（个）由于纸箱的高度与易拉罐的高度相等，因此易拉罐所占空间的总体积与纸箱的容积之比为%794442222hlbrhrlbhlbhrrlb答：纸箱空间的利用率约为79%.小结：1、分式的乘、除法的法则；2、运用法则时注意符号的变化；3、注意因式分解在分式乘除法中的运用；4、分式乘除的结果要化为最简分式或整式。动脑筋动脑筋填空;2ba;3ba;4ba.nbabababababababababa2a2bnbna4b4a3b3a分式的乘方运算分式的乘方,把分子...