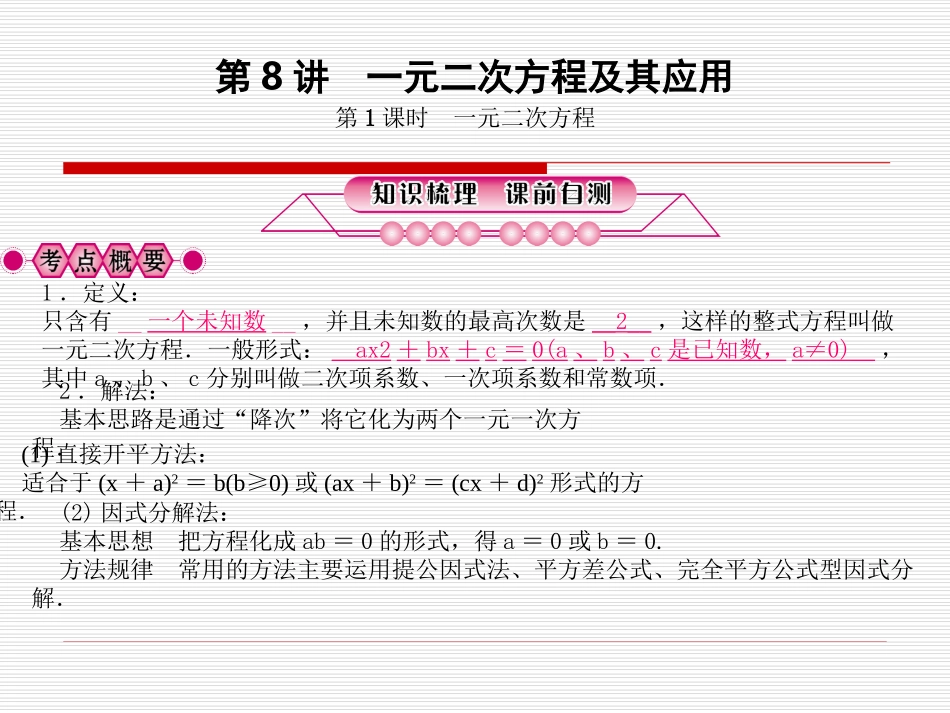
第8讲一元二次方程及其应用1.定义:只含有__一个未知数__,并且未知数的最高次数是__2__,这样的整式方程叫做一元二次方程.一般形式:__ax2+bx+c=0(a、b、c是已知数,a≠0)__,其中a、b、c分别叫做二次项系数、一次项系数和常数项.2.解法:基本思路是通过“降次”将它化为两个一元一次方程.(1)直接开平方法:适合于(x+a)2=b(b≥0)或(ax+b)2=(cx+d)2形式的方程.(2)因式分解法:基本思想把方程化成ab=0的形式,得a=0或b=0.方法规律常用的方法主要运用提公因式法、平方差公式、完全平方公式型因式分解.第1课时一元二次方程(4)配方法:一般步骤①化二次项系数为1;②把常数项移到方程的另一边;③在方程两边同时加上一次项系数一半的平方;④把方程整理成(x+a)2=b的形式;⑤运用直接开平方解方程.3.一元二次方程的根的判别式关于x的一元二次方程ax2+bx+c=0(a≠0)的根的判别式为b2-4ac.(1)b2-4ac>0⇔一元二次方程ax2+bx+c=0(a≠0)有两个不相等的实数根,则x1,2=-b±b2-4ac2a;(2)b2-4ac=0⇔一元二次方程ax2+bx+c=0(a≠0)有两个相等的实数根,即x1=x2=-b2a;(3)b2-4ac<0⇔一元二次方程ax2+bx+c=0(a≠0)没有实数根.“注意:①根的判别式b2-4ac”只有在确认方程为一元二次方程时才能使用;②使用时,必须将一元二次方程转化一般式ax2+bx+c=0,以便确定a、b、c的值.(3)公式法:一元二次方程ax2+bx+c=0,且b2-4ac≥0时,则x1,2=-b±b2-4ac2a.一般步骤①将方程化成ax2+bx+c=0(a≠0)的形式;②确定a,b,c的值;③若b2-4ac≥0,则代入求根公式,得x1,x2;若b2-4ac<0,则方程无实数根.1.(2011·兰州)下列方程中是关于x的一元二次方程的是A.x2+1x2=0B.ax2+bx+c=0C.(x-1)(x+2)=1D.3x2-2xy-5y2=0配方法:配方法解一元二次方程的一般步骤:(1)把常数项移到等号的右边;(2)把二次项的系数化为1;(3)等式两边同时加上一次项系数一半的平方.(C)2.(2013·黄冈)已知一元二次方程x2-6x+C=0有一个根为2,则另一根为A.2B.3C.4D.8(C)3.(2012·宜宾)将代数式x2+6x+2化成(x+p)2+q的形式为A.(x-3)2+11B.(x+3)2-7C.(x+3)2-11D.(x+2)2+4(B)4.(2013·新疆)方程x2-5x=0的解是A.x1=0,x2=-5B.x=5C.x1=0,x2=5D.x=0(C)5.(2013·温州)方程x2-2x-1=0的解是转化的思想:一元二次方程的解法:直接开平方法、配方法、公式法、因式分解法,都是运用了“转化”的思想,把待解决的问题(一元二次方程),通过转化,归结为已解决的问题(一元一次方程),也就是不断地把“未知”转化为“已知”.【解析】(1)②;(2)x1=4,x2=-2.还可以设函数y=x2-2x-8,根据图象得出函数y与x轴的交点坐标,就可以求x的值;(3)四种方法都可以解.【归纳】一元二次方程的概念以及解法.通过阅读,揭示根与系数的关系,并进行运用,利用整体思想,代数式变形,最后代数式求值.类型一一元二次方程的有关概念例1(2013·牡丹江)若关于x的一元二次方程为ax2+bx+5=0(a≠0)的解是x=1,则2013-a-b的值是()A.2018B.2008C.2014D.2012【思路分析】将x=1代入到ax2+bx+5=0中求得a+b的值,然后求代数式的值即可.【答案】 x=1是一元二次方程ax2+bx+5=0的一个根,∴a·12+b·1+5=0,∴a+b=-5,∴2013-a-b=2013-(a+b)=2013-(-5)=2018.故选A.【解后感悟】此题主要是一元二次方程的解,解题的关键是利用方程解的概念,将方程的解代入原方程,采用整体的思想方法,再解关于待定系数的方程,即可求得代数式a+b的值.【问题】给出以下方程①3x+1=0;②x2-2x=8;③1x-3-2x3-x=1.(1)一元二次方程的是__________;(2)求出(1)中的一元二次方程的解,并联想还有其他的解法吗?(3)通过(1)(2)问题解决,你能想到一元二次方程的哪些知识?2.(2013·兰州)用配方法解方程x2-2x-1=0时,配方后得到的方程为A.(x+1)2=0B.(x-1)2=0C.(x+1)2=2D.(x-1)2=2(D)【解析】把方程x2-2x-1=0的常数项移到等号的右边,得到x2-2x=1,方程两边同时加上一次项系数一半的平方,得到x2-2x+1...