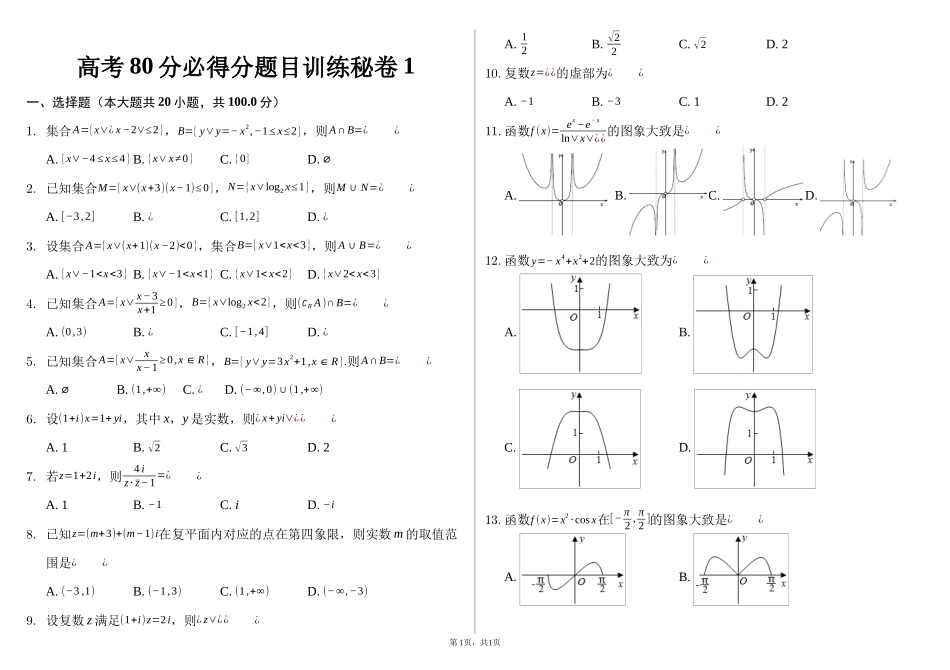
高考80分必得分题目训练秘卷1一、选择题(本大题共20小题,共100.0分)1.集合A={x∨¿x−2∨≤2},B={y∨y=−x2,−1≤x≤2},则A∩B=¿¿A.{x∨−4≤x≤4}B.{x∨x≠0}C.{0}D.⌀2.已知集合M={x∨(x+3)(x−1)≤0},N={x∨log2x≤1},则M∪N=¿¿A.[−3,2]B.¿C.[1,2]D.¿3.设集合A={x∨(x+1)(x−2)<0},集合B={x∨10,∨φ∨¿π2)的图象如图所示,为了得到f(x)的图象,则只要将g(x)=cos2x的图象¿¿A.向右平移π12个单位长度B.向右平移π6个单位长度C.向左平移π12个单位长度D.向左平移π6个单位长度16.将函数f(x)=sin2x的图象保持纵坐标不变,先将横坐标缩短为原来的12,再向右平移π6个单位长度后得到g(x),则g(x)的解析式为¿¿A.g(x)=sin(x−π6)B.g(x)=sin(x+π6)C.g(x)=sin(4x−2π3)D.g(x)=sin(4x−π6)17.△ABC的内角A、B、C的对边分别为a、b、c.已知a=√5,c=2,cosA=23,则b=¿¿A.√2B.√3C.2D.318.若tanα=34,则cos2α+2sin2α=¿¿A.6425B.4825C.1D.162519.函数f(x)=sin(x−π4)(x∈R)的图象的一条对称轴方程是¿¿A.x=0B.x=−π4C.x=π4D.x=π220.函数f(x)=15sin(x+π3)+cos(x−π6)的最大值为¿¿A.65B.1C.35D.15二、填空题(本大题共10小题,共50.0分)21.已知命题p:∀n∈N,n2<2n,则¬p为______.22.已知函数f(x)=¿sinx∨+cosx,现有如下几个命题:①该函数为偶函数;②该函数最小正周期为π2;③该函数值域为[−1,√2];④若定义区间(a,b)的长度为b−a,则该函数单调递增区间长度的最大值为3π4.其中正确命题为______.23.已知m∈R,命题p:对任意实数x,不等式x2−2x−1≥m2−3m恒成立,若¬p为真命题,则m的取值范围是______.24.设实数a>1,b>1.则“aa−b”成立的______条件.¿请用“充分不必要”,“必要不充分”,“充要”,“既不充分也不必要”中第2页,共2页之一填空.¿充要.25.关于函数f(x)=14x+2的性质,有如下四个命题:①函数f(x)的定义域为R;②函数f(x)的值域为(0,+∞);③方程f(x)=x有且只有一个实根;④函数f(x)的图象是中心对称图形.其中正确命题的序号是______.26.若x,y满足约束条件{x−y+1≥0x+y−3≥0x−3≤0,则z=x−2y的最小值为______.27.设x,y满足约束条件{x+2y≤12x+y≥−1x−y≤0,则z=3x−2y的最小值为______.28.若x,y满足约束条件{x−2y−2≤0x−y+1≥0y≤0,则z=3x+2y的最大值为______.29.若x,y满足约束条件{x+y−5≤02x−y−1≥0x−2y+1≤0,则z=2x+y的最小值为______.30.若x,y满足约束条件{x+2y−5≥0x−2y+3≥0x−5≤0,则z=x+y的最大值为______.三、解答题(本大题共6小题,共60.0分)31.已知函数f(x)=1+2√3sinxcosx−2sin2x,x∈R.(1)求函数f(x)的单调区间;(2)若把f(x)向右平移π6个单位得到函数g(x),求g(x)在区间[−π2,0]上的最小值和最大值.32.已知a⃗=(2sinx,cos2x),b⃗=(√3cosx,2),f(x)=a⃗⋅b⃗.(1)求f(x)的最小正周期及单调递减区间;¿求函数f(x)在区间[0,π2]上的最大值和最小值.33.已知向量a⃗=(cosx,sinx),b⃗=(3,−√3),x∈[0,π].(1)若a⃗/¿b⃗,求x的值;(2)记f(x)=a⃗⋅b⃗,求f(x)的最大值和最小值以及对应的x的值.34.已知函数f(x)=¿.(1)求函数f(x)的最小正周期;(2)求函数f(x)在区间[−π4,π4]上的最大值和最小值.第3页,共1页35.已知函数f(x)=√3sin2x+2sin2x.¿Ⅰ¿求函数f(x)的单调增区间;¿Ⅱ¿将函数f(x)的图象向左平移π12个单位,再向下平移1个单位后得到函数g(x)的图象,当x∈[−π6,π3]时,求函数g(x)的值域.36.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,∨φ∨¿π2)的部分图象如图所示.¿Ⅰ¿求函数f(x)的解析式;¿Ⅱ¿求函数f(x)在区间x∈[0,π2]上的最大值和最小值.第4页,共2页