完全平方公式 ()VIP免费

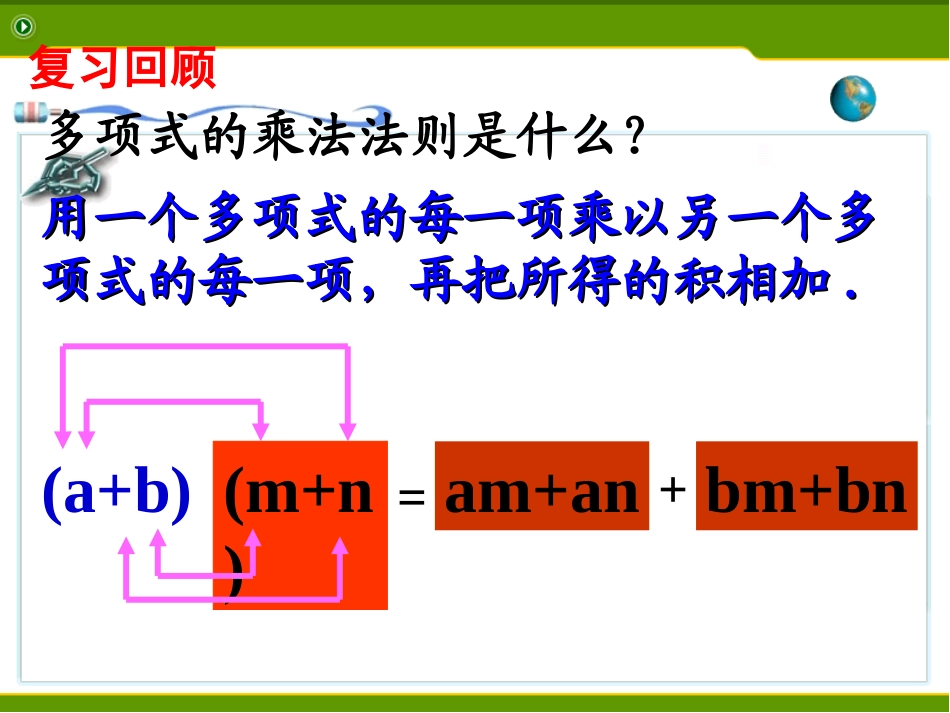
15.2乘法公式---完全平方公式复习回顾用一个多项式的每一项乘以另一个多用一个多项式的每一项乘以另一个多项式的每一项，再把所得的积相加项式的每一项，再把所得的积相加..多项式的乘法法则是什么？am+anbm+bn+=(m+n)(a+b)(a+b)2(a-b)2=a2+2ab+b2=a2-2ab+b2=a2+ab+ab+b2=a2-ab-ab+b2=(a+b)(a+b)=(a-b)(a-b)•计算下列各题:观察以上多项式的乘法,有什么特点?完全平方公式的数学表达式：两个数的和（或差）的平两个数的和（或差）的平方，等于它们的平方和，加上（或方，等于它们的平方和，加上（或减去）它们的积的减去）它们的积的22倍。倍。(a+b)(a+b)22==aa22+b+b22+2ab+2ab(a(a--b)b)22==aa22+b+b22--2ab2ab(a+b)(a+b)22=a=a22+2ab+b+2ab+b22(a(a--b)b)22=a=a22--2ab+b2ab+b22完全平方公式请你尝试用文字概括这个结论。运算形式运算方法（和或差、平方）（平方和、加或减2倍积）(a+b)²a²bbaa2)(ba2ab²2bababab2++完全平方公式的图形理解首平方，尾平方，首尾两倍放中央判断(x+y)2=x2+y2×aabb(a-b)²2)(ba2aab222aabba²ababab2bb²bb完全平方公式的图形理解首平方，尾平方，首尾两倍放中央公式特点：4、公式中的字母a，b可以表示数，单项式和多项式。(a+b)(a+b)22=a=a22+2ab+b+2ab+b22(a(a--b)b)22=a=a22--2ab+b2ab+b221、积为二次三项式；2、积中两项为两数的平方和；3、另一项是两数积的2倍，且与乘式中间的符号相同。首平方，尾平方，首尾两倍放中央完全平方公式下面各式的计算是否正确？如果不正确，应当怎样改正？(1)(x+y)2=x2+y2(2)(x-y)2=x2-y2(3)(x-y)2=x2+2xy+y2(4)(x+y)2=x2+xy+y2错错错错错错错错(x+y)2=x2+2xy+y2(x-y)2=x2-2xy+y2(x-y)2=x2--2xy+y2(x+y)2=x2+22xy+y2感受新知----试一试+(2y)2例1运用完全平方公式计算：解：(x+2y)2==x2(1)(x+2y)2(a+b)(a+b)22=a=a22+2ab+b+2ab+b22x2+2•x•2y+4xy+4y2感受新知----看一看(2)(x-2y)2解：(x-2y)2=x2-2•x•2y+(2y)2=x2(a-b)(a-b)22=a=a22-2ab+b-2ab+b22-4xy+4y2例2运用完全平方公式计算：(1)(4a2-b2)2分析：4a2ab2b解：（4a2－b2）2=()2－2()·()+()2=16a4－8a2b2+b4记清公式、代准数式、准确计算。记清公式、代准数式、准确计算。解题过程分解题过程分33步：步：(a-b)(a-b)22=a=a22-2ab+b-2ab+b224a24a2b2b2(2)(x–2y2)2+(2y2)2解：(x–2y2)2=(a(a--b)b)22=a=a22--2ab+b2ab+b22(x)2–2•(x)•(2y2)12121212=x2–2xy2+4y414(3)(a2+b3)2(-b+a)(-b+a)22=(a-b)=(a-b)222332解：原式=(b3a2)22332(a2+b3)2=(b3-a2)223233232=b6-2a2b3+a44994(4)(-x2y-)2解：原式=(x2y+)2=x4y2+x2y+(-a-b)(-a-b)22=(a+b)=(a+b)22323214143494116计算：（1）(x-3)2（2）(2m-n)2（3）(-2m+n)2（4）(-2m-n)2x2-6x+94m2-4mn+n24m2-4mn+n24m2+4mn+n2练习例3运用完全平方公式计算：(1)1042解：1042=(100+4)2=10000+800+16=10816(2)99.992解：99.992=(100–0.01)2=10000-2+0.0001=9998.0001如何运用完全平方公式使计算更简便(1)(-a+b)2(2)(-2m-1)2(3)(2x+5)(-2x-5)(4)(x+y-1)2=(b-a)2=-(2m+1)2=(2m+1)2=-(2x+5)(2x+5)=-(2x+5)2=(x+y)-12添括号时,如果括号前面是正号,括到括号里的各项都不变号;如果括号前面是负号,括到括号里的各项都改变符号.a+(b+c)=a+b+c;a-(b+c)=a-b–c.a+b+c=a+(b+c);a–b–c=a–(b+c).例41.运用乘法公式计算:(1)(x+2y-3)(x-2y+3);(2)(a+b+c)2.解:(1)(x+2y-3)(x-2y+3)=[x+(2y–3)][x-(2y-3)]=x2-(2y-3)2=x2-(4y2-12y+9)=x2-4y2+12y-9.(2)(a+b+c)2=[(a+b)+c]2=(a+b)2+2(a+b)c+c2=a2+2ab+b2+2ac+2bc+c2=a2+b2+c2+2ab+2bc+2ac.（x+2y+3)(x-2y+3)=？（a+b-c)2=？2.运用乘法公式计算:(1)(a+2b–1)2;(2)(2x+y+z)(2x–y–z)3.如图,一块直径为a+b的圆形钢板,从中挖去直径分别为a与b的两个圆,求剩下的钢板的面积.1、代数式2xy-x2-y2=()A.(x-y)2B.(-x-y)2C.(y-x)2D.-(x-y)2D2、如果x2-6xy+N是一个完全平方式,那么N为________3、如果4x2+mxy+9y2是一个完全平方式,那么m的值是____________9y2±12练习(a+b)(a+b)2_2_aa2_2_bb22=______=______(a(a--b)b)22+2ab=______+2ab=______公式变形(a-b)(a-b)22+4ab=__...