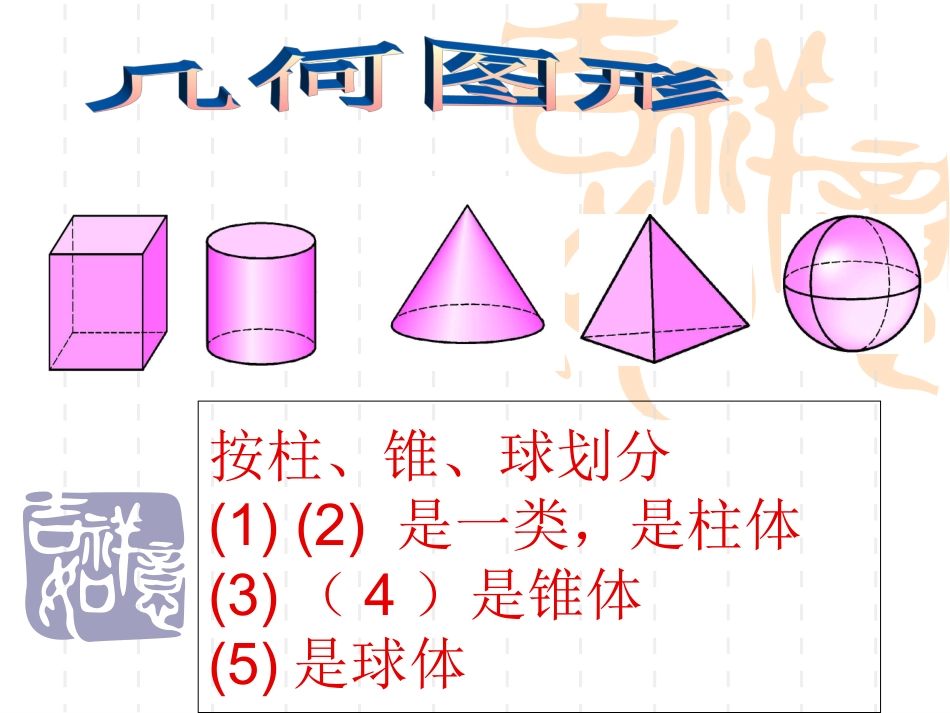
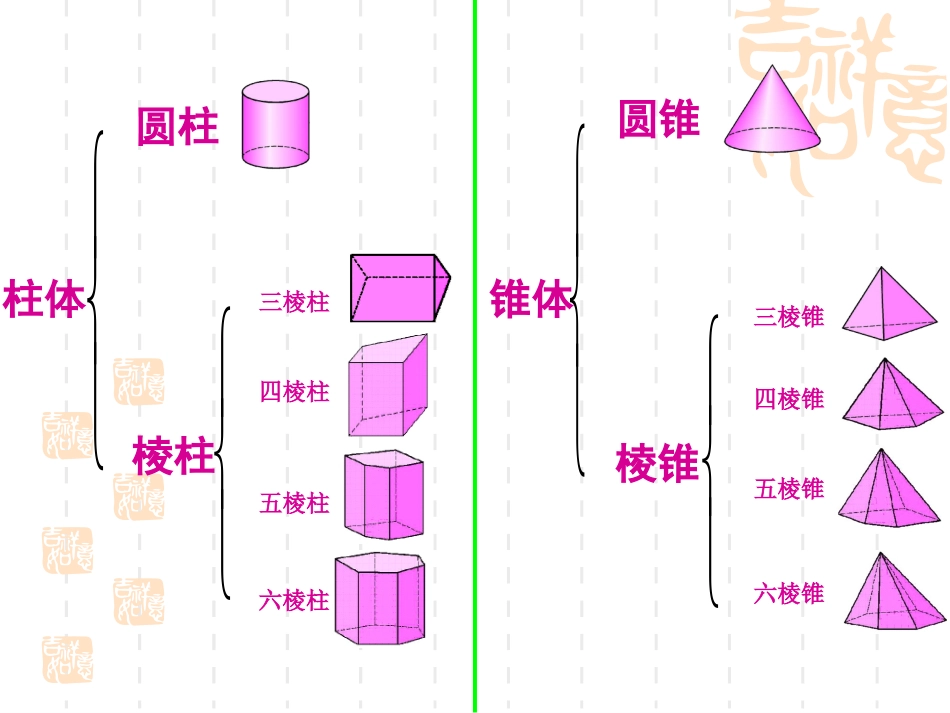
第四章(综合复习课)第四章(综合复习课)按柱、锥、球划分(1)(2)是一类,是柱体(3)(4)是锥体(5)是球体柱体锥体圆柱棱柱圆锥棱锥四棱柱六棱柱五棱柱三棱柱四棱锥五棱锥六棱锥三棱锥从不同的方向看正方体长方体四棱锥三棱柱三棱柱三棱柱五棱锥五棱锥归纳:正方体的表面展开图有以下11种。你能看出有什么规律吗?一四一型二三一型阶梯型点和线A点A——用一个大写字母表示。线线段直线射线学会区分没有直线、射线、线段的比较直线、射线、线段的比较直线、射线、线段的比较直线、射线、线段的比较名称线段射线直线图形aABlOClAB表示法线段AB、线段BA、线段a射线OC、射线l直线AB、直线BA、直线l延伸性无沿OC方向延伸向两方无限延伸端点个数210作图叙述连接AB以点O为端点作射线OC过A、B两点作直线AB线段的基本性质:两点之间线段最短.下面的知识点你掌握了吗?直线的基本性质:经过两点有一条直线并且只有一条直线.两点间的距离:连结两点的线段的长度,叫做这两点间的距离.用一个钉子把一根细木条钉在木板上,用手拔木条,木条能转动,这表明_______________;用两个钉子把细木条钉在木板上,就能固定细木条,这说明________________。过一点有无数条直线两点确定一条直线应用举例线段中点的定义●●●ACBABCBAC21或AB=2AC=2CB(1)已知AC=8cm,CB=6cm,如果O是线段AB的中点,求线段OC的长度。ABCOABCO(2)已知AB=16cm,C是直线AB上一点,且AC=10cm,D为AC的中点,E是BC的中点,求线段DE的长。把长方形的一角折叠得到折痕EF,如图1,((FEDCBA如图1A(FBDE(C)(G如图2再沿FG折叠,使得C、E重合,如图2所示,已知∠EFG=,求∠BFE的度数75G认真想一想1、如图、线段AB=14cm,C是AB上一点,且AC=9cm,O是AB的中点,求线段OC的长度。21解:∵点O是线段AB的中点,AB=14㎝∴AO=AB=7㎝∴OC=AC-AO=9㎝-7㎝=2㎝认真解一解2、如图,已知∠AOB=90°,∠AOC是60°,OD平分∠BOC,OE平分∠AOC。求∠DOE。解:∵∠AOB=90°,∠AOC=60°∴∠BOC=∠AOB+∠AOC=150°∵OD平分∠BOC∴∠DOC=21∠BOC=75°同理∠EOC=AOC=30°∠21∴∠EOD=∠COD-∠EOC=75°-30°=45°3、如果两个角互补,并且它们的差是30°,那么较大的角等于.105°4.一个角的余角比它的补角的一半还少30°,求这个角.5.一个角的补角是123°24′16″,则这个角的余角是多少?33°24′16″60度6.如图,已知直线AB和CD相交于O点,CO∠E是直角,OF平分∠AOE,COF=34°,∠求∠BOD的度数.CBAEODF22度作业布置课本P152—P156第1—16题;教与学:第四章自我评价