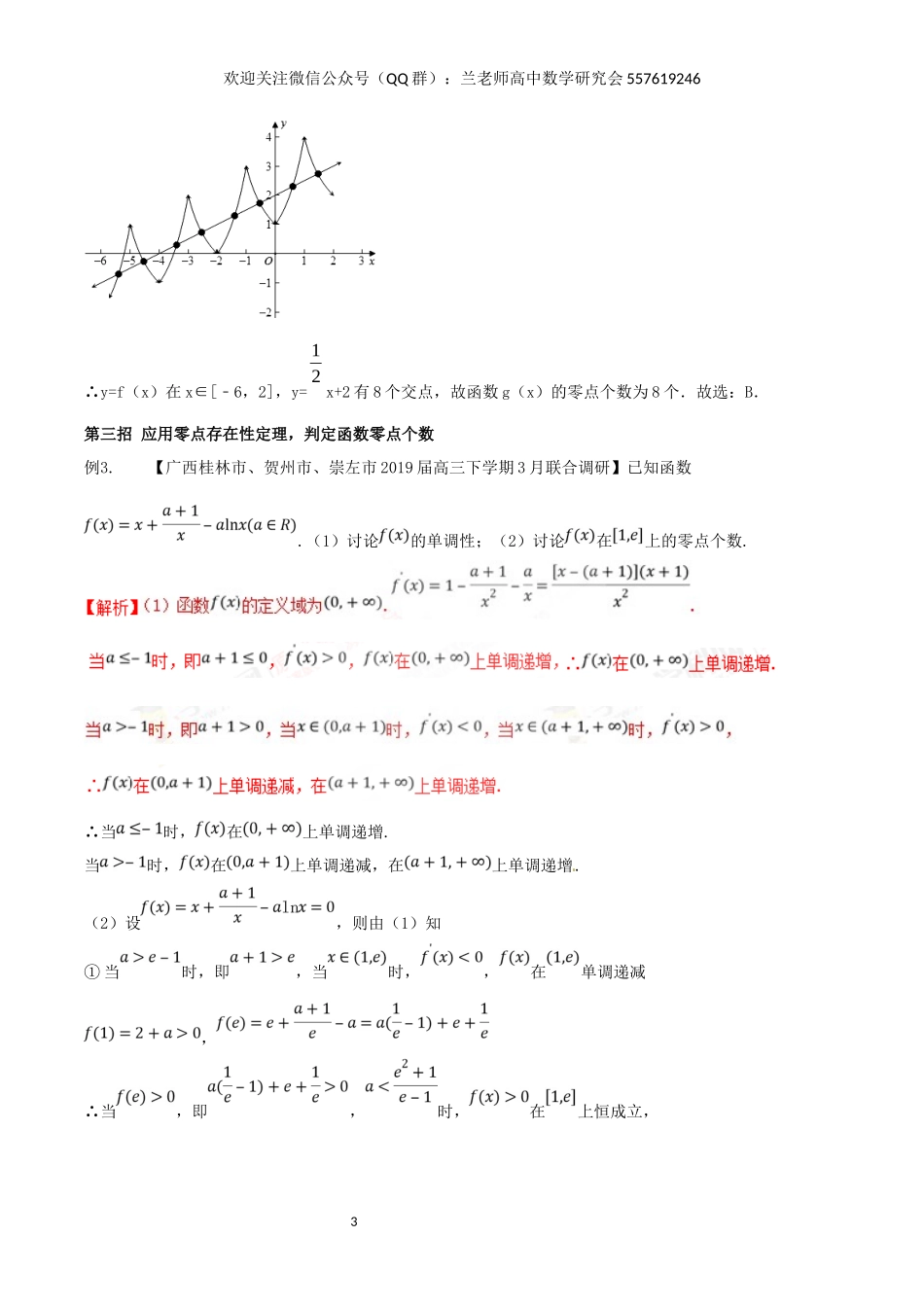
1欢迎关注微信公众号(QQ群):兰老师高中数学研究会557619246专题一“四招”判断函数零点个数函数方程思想是一种重要的数学思想方法,函数问题可以利用方程求解,方程解的情况可借助于函数的图象和性质求解.高考命题常常以基本初等函数为载体,主要考查以下三个方面:(1)零点所在区间——零点存在性定理;(2)二次方程根的分布问题;(3)判断零点的个数问题;(4)根据零点的情况确定参数的值或范围;(5)根据零点的情况讨论函数的性质或证明不等式等.本专题围绕函数零点个数的判断问题,例题说法,高效训练.【典型例题】第一招应用函数性质,判定函数零点个数例1.已知偶函数4log,04{8,48xxfxfxx,且8fxfx,则函数12xFxfx在区间2018,2018的零点个数为()A.2020B.2016C.1010D.1008【答案】A【解析】,当08x时,函数fx与函数12xy图象有4个交点2欢迎关注微信公众号(QQ群):兰老师高中数学研究会557619246201825282,由4211122242flog知,当02x时函数fx与函数12xy图象有2个交点故函数Fx的零点个数为2524222020,故选A.第二招数形结合,判定函数零点个数例2.【2018届福建省永春一中、培元、季延、石光中学四校高三上第二次联考】定义在R上的函数fx满足21fxfx,且0,1x时,4xfx;1,2x时,1ffxx.令24,6,2gxfxxx,则函数gx的零点个数为()A.7B.8C.9D.10【答案】B, 函数f(x)满足f(x+2)=f(x)+1,即自变量x每增加2个单位,函数图象向上平移1个单位,自变量每减少2个单位,函数图象向下平移1个单位,分别画出函数y=f(x)在x∈[﹣6,2],y=12x+2的图象,3欢迎关注微信公众号(QQ群):兰老师高中数学研究会557619246∴y=f(x)在x∈[﹣6,2],y=12x+2有8个交点,故函数g(x)的零点个数为8个.故选:B.第三招应用零点存在性定理,判定函数零点个数例3.【广西桂林市、贺州市、崇左市2019届高三下学期3月联合调研】已知函数.(1)讨论的单调性;(2)讨论在上的零点个数.∴当时,在上单调递增.当时,在上单调递减,在上单调递增.(2)设,则由(1)知①当时,即,当时,,在单调递减,∴当,即,时,在上恒成立,4欢迎关注微信公众号(QQ群):兰老师高中数学研究会557619246∴当时,在内无零点.当,即,时,,根据零点存在性定理知,此时,在内有零点, 在内单调递减,∴此时,在有一个零点.②当时,即,当时,,在单调递增,,.∴当,即时,,根据零点存在性定理,此时,在内有零点. 在内单调递增,∴此时,在有一个零点.当时,,∴此时,在无零点.③当时,即,当时,;当时,;则在单调递减,在单调递增.∴在上恒成立,∴此时,在内无零点.∴综上所述:当时,在内有1个零点;当时,在有一个零点;当时,在无零点.第四招构造函数,判定函数零点个数例4.【山东省菏泽市2019届高三上学期期末】已知函数f(x)=lnx+﹣1,a∈R.(1)当a>0时,若函数f(x)在区间[1,3]上的最小值为,求a的值;(2)讨论函数g(x)=f′(x)﹣零点的个数.5欢迎关注微信公众号(QQ群):兰老师高中数学研究会557619246f’(x)min=f(a)=lna,令,得.当a≥3时,f’(x)<0在(1,3)上恒成立,这时f(x)在[1,3]上为减函数,∴,令得a=4﹣3ln3<2(舍去).综上知.(2) 函数,令g(x)=0,得.设,,当x∈(0,1)时,φ'(x)>0,此时φ(x)在(0,1)上单调递增,当x∈(1,+∞)时,φ’(x)<0,此时φ(x)在(1,+∞)上单调递减,所以x=1是φ(x)的唯一极值点,且是极大值点,因此x=1也是(x)的最大值点,φ(x)的最大值为.又φ(0)=0,结合φ(x)的图象可知:①当时,函数g(x)无零点;6欢迎关注微信公众号(QQ群):兰老师高中数学研究会557619246②当时,函数g(x)有且仅有一个零点;③当时,函数g(x)有两个零点;④a≤0时,函数g(x)有且只有一个零点;综上所述,当时,函数g(x)无零点;当或a≤0时,函数g(x)有且仅有一个零点;当时,函数g(x)有两个零点.【规律...