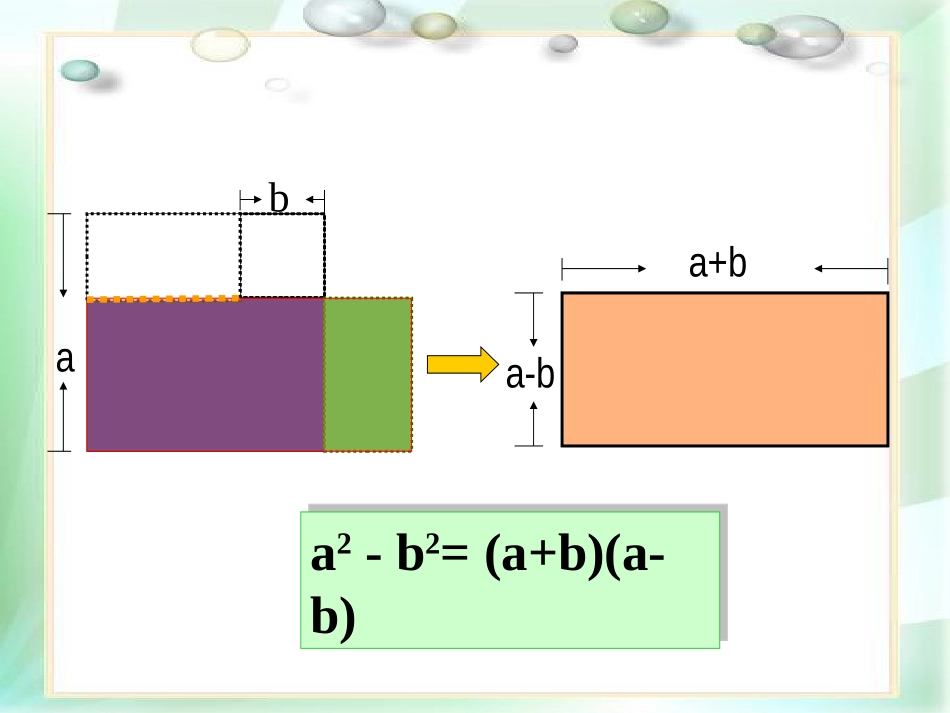
大麻中学:方家祚ba如图:边长为a的正方形一角剪去一个边长为b的小正方形,请你动手将这个图形剪切,拼成一个四边形。a-ba+baba2-b2=(a+b)(a-b)a2-b2=(a+b)(a-b)a-ba+baba2-b2=(a+b)(a-b)a2-b2=(a+b)(a-b)aba-b2b2aa2-b2=(2a+2b)(a-b)=(a+b)(a-b)a2-b2=(2a+2b)(a-b)=(a+b)(a-b)12平方差公式反过来就是说:两个数的平方差,等于这两个数的和与这两个数的差的积a²-b²=(a+b)(a-b)因式分解整式乘法平方差公式:(a+b)(a-b)=a²-b²(甲+乙)(甲-乙)=甲²-乙²甲²-乙²=(甲+乙)(甲-乙)整式乘法:因式分解:提示:上面面式子中的甲、乙可以代表一个数也可以是一个式子,整式乘法和因式分解是互逆运算。把下列各式分解因式(1)x²-1(2)m²-9(4)x²-0.04y²=(x+1)(x-1)=(m+3)(m-3)=(x+2y)(x-2y)平方差公式:a2-b2=(a+b)(a-b)(3)x²-4y²(5)4x²-9y²=(2x+3y)(2x-3y)=(x+0.2y)(x-0.2y)=m²-3²=x²-1²=x²-(2y)²=x²-(0.2y)²=(2x)²-(3y)²例:把下列各式分解因式(1)16x²-1(2)25a²-9c²(3)-m²+4n²(4)–n²m²+4=(5a+3c)(5a-3c)=(2-mn)(2+mn)=(2n+m)(2n-m)=(4x+1)(4x-1)=4n²-m²=4–n²m²做一做:下列多项式可以用平方差公式分解因式吗?思考:用平方差公式分解因式时,因式应具备怎样的思考:用平方差公式分解因式时,因式应具备怎样的形式?形式?(1)x²-y²(2)x²+y²(3)-x²+y²(4)-x²-y²(5)(-x)²+(-y)²(6)-x²-(-y)²例2.把下列各式分解因式①x4-81y4②2a³-8a1.解:原式=(x²+9y²)(x²-9y²)=(x²+9y²)(x+3y)(x-3y)2.解:原式=2a(a2-4)=2a(a+2)(a-2)1.有公因式首先要提取公因式.2.再应用平方差公式分解3.每个因式要化简,并且分解彻底对于分解复杂的多项式,我们应该怎么做?课堂练习.把下列各式分解因式(2)x3y-9xy3(1)x4-1(3)(m+n)2-(m-n)2=(x2+1)(x2-1)=(x2+1)(x+1)(x-1)=xy(x2-9y2)=xy(x+3y)(x-3y)=[(m+n)+(m-n)][(m+n)-(m-n)]=(m+n+m-n)(m+n-m+n)=2m·2n=4mn通过本节课的学习,你有哪些收获?分解因式的步骤:(1)有公因式一定要先提取公因式(2)其次看是否能用公式法(3)检查是否分解彻底了计算(1)20052-20042解:20052-20042(2)2×552-452×2=(2005+2004)(2005-2004)=4009=2×(55+45)(55-45)解:原式=2×(552-452)=2×100×10=2000拓展训练1分解因式:(1)(a+b+c)²-(a–b+c)²=(a+b+c+a-b+c)(a+b+c-a+b-c)=[(a+b+c)+(a-b+c)][(a+b+c)-(a-b+c)]拓展训练2=(2a+2c)·2b=4b(a+c)拓展训练3(课后思考)小明在使用计算器是发现一个规律,连续的两个基数的平方差总是8的倍数,他感到很困惑,你能帮助他想想为什么?